Question

【题目】已知函数f（x）是定义在R上的偶函数，且当x≤0时，f（x）=x2+2x．
（1）现已画出函数f（x）在y轴左侧的图象，如图所示，请补全函数f（x）的图象，并根据图象写出函数f（x）（x∈R）的递增区间；

（2）写出函数f（x）（x∈R）的值域；
（3）写出函数f（x）（x∈R）的解析式．

Answer 1

【答案】
（1）解：根据偶函数的图象关于y轴对称，作出函数在R上的图象，

结合图象可得函数的增区间为（﹣1，0）、减区间为（1，+∞）

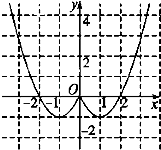
（2）解：结合函数的图象可得，当x=1，或 x=﹣1时，函数取得最小值为﹣1，

函数没有最大值，故函数的值域为[﹣1，+∞）

（3）解：当x＞0时，﹣x＜0，再根据x≤0时，f（x）=x2+2x，

可得f（﹣x）=（﹣x）2+2（﹣x）=x2﹣2x．

再根据函数f（x）为偶函数，可得f（x）=x2﹣2x．

综上可得，f（x）=

【解析】（1）根据偶函数的图象关于y轴对称，作出函数在R上的图象，结合图象可得函数的增区．（2）结合函数的图象可得函数的值域．（3）依据条件求得当x＞0时，f（x）的解析式，再依据函数的奇偶性得到f（x）在R上的解析式．
【考点精析】通过灵活运用函数的值域和函数图象的作法，掌握求函数值域的方法和求函数最值的常用方法基本上是相同的．事实上，如果在函数的值域中存在一个最小（大）数，这个数就是函数的最小（大）值．因此求函数的最值与值域，其实质是相同的；图象的作法与平移：①据函数表达式，列表、描点、连光滑曲线；②利用熟知函数的图象的平移、翻转、伸缩变换；③利用反函数的图象与对称性描绘函数图象即可以解答此题．