
【题目】如图所示,在四棱锥P-ABCD中,底面是边长为1的正方形,侧棱PD=1,PA=PC=![]() .
.
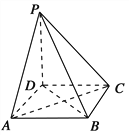
(1)求证:PD⊥平面ABCD;
(2)求证:平面PAC⊥平面PBD;
 口算题卡河北少年儿童出版社系列答案
口算题卡河北少年儿童出版社系列答案 A加金题 系列答案
A加金题 系列答案 全优测试卷系列答案
全优测试卷系列答案科目:高中数学 来源: 题型:
【题目】已知关于![]() 的不等式
的不等式![]() 的解集为
的解集为![]() .
.
(1)若![]() 是从
是从![]() 四个数中任取的一个数,
四个数中任取的一个数, ![]() 是从
是从![]() 三个数中任取的一个数,求
三个数中任取的一个数,求![]() 不为空集的概率;
不为空集的概率;
(2)若![]() 是从区间
是从区间![]() 上任取的一个数,
上任取的一个数, ![]() 是从区间
是从区间![]() 上任取的一个数,求
上任取的一个数,求![]() 不为空集的概率.
不为空集的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了解今年某校高三毕业班想参军的学生体重情况,将所得的数据整理后,画出了频率分布直方图(如图).已知图中从左到右的前3个小组的频率之比为1:2:3,其中第2小组的频数为24.
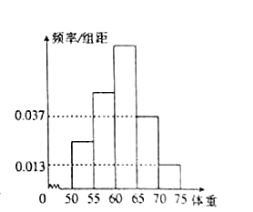
(Ⅰ)求该校高三毕业班想参军的学生人数;
(Ⅱ)以这所学校的样本数据来估计全省的总体数据,若从全省高三毕业班想参军的同学中(人数很多)任选三人,设![]() 表示体重超过60公斤的学生人数,求
表示体重超过60公斤的学生人数,求![]() 的分布列和数学期望.
的分布列和数学期望.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线![]() :
:![]() (
(![]() )与椭圆
)与椭圆![]() :
:![]() 相交所得的弦长为
相交所得的弦长为![]() .
.
(Ⅰ)求抛物线![]() 的标准方程;
的标准方程;
(Ⅱ)设![]() ,
,![]() 是
是![]() 上异于原点
上异于原点![]() 的两个不同点,直线
的两个不同点,直线![]() 和
和![]() 的倾斜角分别为
的倾斜角分别为![]() 和
和![]() ,当
,当![]() ,
,![]() 变化且
变化且![]() 为定值
为定值![]() (
(![]() )时,证明:直线
)时,证明:直线![]() 恒过定点,并求出该定点的坐标.
恒过定点,并求出该定点的坐标.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】连江一中第49届田径运动会提出了“我运动、我阳光、我健康、我快乐”的口号,某同学要设计一张如图所示的竖向张贴的长方形海报进行宣传,要求版心面积为162 ![]() (版心是指图中的长方形阴影部分,
(版心是指图中的长方形阴影部分,![]() 为长度单位分米),上、下两边各空2
为长度单位分米),上、下两边各空2 ![]() ,左、右两边各空1
,左、右两边各空1 ![]() .
.

(Ⅰ)若设版心的高为![]()
![]() ,求海报四周空白面积关于
,求海报四周空白面积关于![]() 的函数
的函数![]() 的解析式;
的解析式;
(Ⅱ)要使海报四周空白面积最小,版心的高和宽该如何设计?
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=lg(ax2+2x+1) .
(1)若函数f (x)的定义域为R,求实数a的取值范围;
(2)若函数f (x)的值域为R,求实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com