
【题目】设a为实数,函数f(x)=x2+|x-a|+1,x∈R.
(1)讨论f(x)的奇偶性;
(2)求f(x)的最小值.
【答案】(1)当![]() 时,
时, ![]() 偶函数,当
偶函数,当![]() 时,
时, ![]() 为非奇非偶函数;(2)
为非奇非偶函数;(2)![]() .
.
【解析】试题分析:(1)对于函数 f(x)=x2+|x﹣a|+1,分当a=0时、和当a≠0时两种情况,分别讨论f(x)的奇偶性;
(2)当x≤a时,f(x)=x2﹣x+a+1=(x﹣![]() )2+a+
)2+a+![]() ,分a>
,分a>![]() 时和a≤
时和a≤![]() 时两种情况,分别求得函数f(x)的最小值.②当x>a 时,f(x)=x2+x﹣a+1=(x+
时两种情况,分别求得函数f(x)的最小值.②当x>a 时,f(x)=x2+x﹣a+1=(x+![]() )2﹣a+
)2﹣a+![]() ,分a>﹣
,分a>﹣![]() 时和当a≤﹣
时和当a≤﹣![]() 时两种情况,分别求得函数f(x)的最小值.
时两种情况,分别求得函数f(x)的最小值.
解:(1)对于函数 f(x)=x2+|x﹣a|+1,
当a=0时,f(x)=x2+|x|+1为偶函数,
当a≠0时,f(x)=x2+|x|+1为非奇非偶函数.
(2)①当x≤a时,f(x)=x2﹣x+a+1=(x﹣![]() )2+a+
)2+a+![]() ,
,
若a>![]() 时,函数f(x)的最小值为f(
时,函数f(x)的最小值为f(![]() )=a+
)=a+![]() ;
;
若a≤![]() 时,函数f(x)的最小值为f(a)=a2+1.
时,函数f(x)的最小值为f(a)=a2+1.
②当x>a 时,f(x)=x2+x﹣a+1=(x+![]() )2﹣a+
)2﹣a+![]() ,
,
若a>﹣![]() 时,函数f(x)的最小值为f(a)=a2+1;
时,函数f(x)的最小值为f(a)=a2+1;
若a≤﹣![]() 时,函数f(x)的最小值为f(﹣
时,函数f(x)的最小值为f(﹣![]() )=﹣a+
)=﹣a+![]() .
.


 小学课时特训系列答案
小学课时特训系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆E: ![]() 经过点
经过点 ,离心率为
,离心率为![]() .
.
(1)求椭圆E的标准方程;
(2)若A1,A2分别是椭圆E的左、右顶点,过点A2作直线l与x轴垂直,点P是椭圆E上的任意一点(不同于椭圆E的四个顶点),连接PA1交直线l于点B,点Q为线段A2B的中点,求证:直线PQ与椭圆E只有一个公共点.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C: ![]() (a>b>0),长轴长为4,离心率为
(a>b>0),长轴长为4,离心率为![]() .
.
(Ⅰ)椭圆的求椭圆的标准方程;
(Ⅱ)设过定点M(0,2)的直线l与椭圆C交于不同的两点A,B,且∠AOB为锐角(O为坐标原点),求直线l的斜率k的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856261)
某企业员工500人参加“学雷锋”志愿活动,按年龄分组:第1组![]() ,第2组
,第2组![]() ,第3组
,第3组![]() ,第4组
,第4组![]() ,第5组
,第5组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(Ⅰ)下表是年龄的频率分布表,求正整数a,b的值;

(Ⅱ)现在要从年龄较小的第1,2,3组中用分层抽样的方法抽取6人,年龄在第1,2,3组抽取的员工的人数分别是多少?
(Ⅲ)在(Ⅱ)的前提下,从这6人中随机抽取2人参加社区宣传交流活动,求至少有1人年龄在第3组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
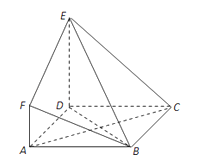
【题目】如图,ABCD是边长为3的正方形,DE⊥平面ABCD,AF∥DE,DE=3AF,BE与平面ABCD所成角为60°.
(Ⅰ)求证:AC⊥平面BDE;
(Ⅱ)求二面角F﹣BE﹣D的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=(2x+b)ex,F(x)=bx-ln x,b∈R.
(1)若b<0,且存在区间M,使f(x)和F(x)在区间M上具有相同的单调性,求实数b的取值范围;
(2)若F(x+1)>b对任意x∈(0,+∞)恒成立,求实数b的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对2000名高一新生进行英语特长测试选拔,现抽取部分学生的英语成绩,将所得数据整理后得出频率分布直方图如图所示,图中从左到右各小长方形面积之比为![]() ,第二小组频数为12.
,第二小组频数为12.
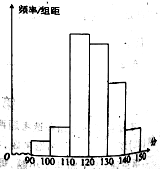
(Ⅰ)求第二小组的频率及抽取的学生人数;
(Ⅱ)若分数在120分以上(含120分)才有资格被录取,约有多少学生有资格被录取?
(Ⅲ)学校打算从分数在![]() 和
和![]() 分内的学生中,按分层抽样抽取4人进行改进意见问卷调查,若调查老师随机从这4人的问卷中(每人一份)随机抽取两份调阅,求这两份问卷都来自英语测试成绩在
分内的学生中,按分层抽样抽取4人进行改进意见问卷调查,若调查老师随机从这4人的问卷中(每人一份)随机抽取两份调阅,求这两份问卷都来自英语测试成绩在![]() 分的学生的概率.
分的学生的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线C:y2=ax(a>0)上一点P(t, ![]() )到焦点F的距离为2t.
)到焦点F的距离为2t.
(l)求抛物线C的方程;
(2)抛物线上一点A的纵坐标为1,过点Q(3,﹣1)的直线与抛物线C交于M,N两个不同的点(均与点A不重合),设直线AM,AN的斜率分别为k1,k2,求证:k1×k2为定值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(导学号:05856325)已知函数f(x)=![]() +eln x,直线l:y=kx(k≠0)与函数f(x)的图象相切于点A(t,f(t))(f(t)≠0),则( )
+eln x,直线l:y=kx(k≠0)与函数f(x)的图象相切于点A(t,f(t))(f(t)≠0),则( )
A. t∈(0,1) B. t∈(1,e) C. t∈(e,3) D. t∈(3,e2)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com