
【题目】如图所示的几何体,关于其结构特征,下列说法不正确的是
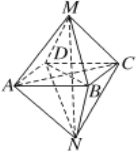
A. 该几何体是由两个同底的四棱锥组成的几何体
B. 该几何体有12条棱、6个顶点
C. 该几何体有8个面,并且各面均为三角形
D. 该几何体有9个面,其中一个面是四边形,其余均为三角形
 愉快的寒假南京出版社系列答案
愉快的寒假南京出版社系列答案科目:高中数学 来源: 题型:
【题目】已知抛物线E:y2=4x,设A、B是抛物线E上分别位于x轴两侧的两个动点,且 ![]()
![]() =
= ![]() (其中O为坐标原点)
(其中O为坐标原点)
(Ⅰ)求证:直线AB必过定点,并求出该定点Q的坐标;
(Ⅱ)过点Q作AB的垂线与抛物线交于G、D两点,求四边形AGBD面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在△ABC中,角A,B,C的对边分别为a,b,c,已知 ![]() cosB+
cosB+ ![]() cosA=
cosA= ![]() (I)求∠C的大小;
(I)求∠C的大小;
(II)求sinB﹣ ![]() sinA的最小值.
sinA的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四面体![]() 中,
中, ![]() 平面
平面![]() ,
, ![]() ,
, ![]() ,
,
![]() 为
为![]() 的中点.
的中点.

(Ⅰ)求证: ![]() ;
;
(Ⅱ)求二面角![]() 的余弦值.
的余弦值.
(Ⅲ)求四面体![]() 的外接球的表面积.
的外接球的表面积.
(注:如果一个多面体的顶点都在球面上,那么常把该球称为多面体的外接球. 球的表面积![]() )
)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知实数x,y满足 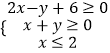 ,若目标函数z=﹣mx+y的最大值为﹣2m+10,最小值为﹣2m﹣2,则实数m的取值范围是( )
,若目标函数z=﹣mx+y的最大值为﹣2m+10,最小值为﹣2m﹣2,则实数m的取值范围是( )
A.[﹣1,2]
B.[﹣2,1]
C.[2,3]
D.[﹣1,3]
查看答案和解析>>
科目:高中数学 来源: 题型:
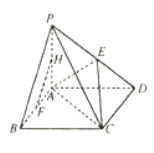
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 为矩形,
为矩形, ![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 的中点,
的中点, ![]() 是
是![]() 中点.
中点.
(1)证明: ![]() 平面
平面![]() ;
;
(2)若平面![]() 底面
底面![]() ,
, ![]() ,试在
,试在![]() 上找一点
上找一点![]() ,使
,使![]() 平面
平面![]() ,并证明此结论.
,并证明此结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,正方形ABCD的中心为O , 四边形OBEF为矩形,平面OBEF⊥平面ABCD , 点G为AB的中点,AB=BE=2.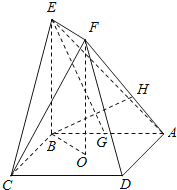
(1)求证:EG∥平面ADF;
(2)求二面角O-EF-C的正弦值;
(3)设H为线段AF上的点,且AH= ![]() HF , 求直线BH和平面CEF所成角的正弦值.
HF , 求直线BH和平面CEF所成角的正弦值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com