练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】若角是第一象限角，问角（1），（2），（3）各是第几象限角？

    【答案】（1）是第一或第二象限角或是终边重合于轴的非负半轴的角；（2）是第一或第三象限角；（3）是第一或第二或第三象限角.

    【解析】

    （1）由可得，可得答案；

    （2）由得，再对整数分类讨论，可得答案；

    （3）由得，再对分类讨论，可得答案.

    （1）∵是第一象限角，

    ∴（*）

    ∴.

    故是第一或第二象限角或是终边重合于轴的非负半轴的角.

    （2）由（*）得.

    ①当为偶数时，令，

    得，这表明是第一象限角.

    ②当为奇数时，令，

    得，这表明是第三象限角.

    综合①②知，是第一或第三象限角.

    （3）由（*）得.

    ①当时，，这表明是第一象限角.

    ②当时，，这表明是第二象限角.

    ③当时，，这表明是第三象限角.

    综合①②③知，是第一或第二或第三象限角.

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数，.

    （1）当时，方程在区间内有唯一实数解，求实数的取值范围；

    （2）对于区间上的任意不相等的实数、，都有成立，求的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】山东省于2015年设立了水下考古研究中心，以此推动全省的水下考古、水下文化遗产保护等工作;水下考古研究中心工作站，分别设在位于刘公岛的中国甲午战争博物院和威海市博物馆。为对刘公岛周边海域水底情况进行详细了解，然后再选择合适的时机下水探摸、打捞，省水下考古中心在一次水下考古活动中，某一潜水员需潜水米到水底进行考古作业，其用氧量包含以下三个方面：

    ①下潜平均速度为米/分钟，每分钟的用氧量为升；

    ②水底作业时间范围是最少10分钟最多20分钟，每分钟用氧量为0.4升；

    ③返回水面时，平均速度为米/分钟，每分钟用氧量为0.32升.

    潜水员在此次考古活动中的总用氧量为升.

    （Ⅰ）如果水底作业时间是分钟，将表示为的函数；

    （Ⅱ）若，水底作业时间为20分钟，求总用氧量的取值范围.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （1）当时，求函数的图像在出的切线方程；

    （2）判断函数的单调性；

    （3）证明：.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】从某网站的程序员中随机抽取名统计其年龄数据如下表：

    年龄

    23

    26

    27

    30

    32

    34

    38

    人数

    1

    3

    3

    5

    4

    3

    1

    （1）求这名程序员的平均年龄及年龄的众数、中位数；

    （2）若这名程序员中年龄不超过岁，且学历是研究生及其以上有人，岁以上且学历是本科及其以下有人，完成下面的列联表，并判断是否有%的把握认为该网站程序员的学历与年龄有关.

    年龄≤30

    年龄>30

    学历研究生及其以上

    学历本科及其以下

    附：

    0.15

    0.10

    0.05

    0.025

    0.01

    0.005

    0.001

    2.072

    2.706

    3.841

    5.024

    6.635

    7.879

    10.828

    .

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】若对任意的正整数，集合的任意元子集中，总有三个元素两两互素.求的最小值.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点P是抛物线C:上任意一点，过点P作直线PH⊥x轴，点H为垂足.点M是直线PH上一点，且在抛物线的内部，直线l过点M交抛物线C于A、B两点，且点M是线段AB的中点.

    （1）证明：直线l平行于抛物线C在点P处切线；

    （2）若|PM|=, 当点P在抛物线C上运动时，△PAB的面积如何变化？

    查看答案和解析>>

    科目：高中数学 来源： 题型：

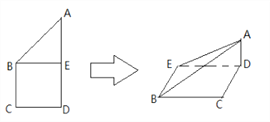
    【题目】如图所示，正方形的边长为，已知，将沿边折起，折起后点在平面上的射影为点，则翻折后的几何体中有如下描述：①与所成角的正切值为；②；③；④平面平面，其中正确的命题序号为___________．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】圆台的上、下底面半径分别为、，母线长，从圆台母线的中点拉一条绳子绕圆台侧面转到点（在下底面），求：

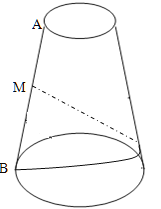
    （1）绳子的最短长度；

    （2）在绳子最短时，上底圆周上的点到绳子的最短距离．

    查看答案和解析>>

    同步练习册答案