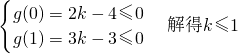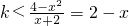已知函数f(x)=ax3+bx2+cx是R上的奇函数,且f(1)=2,f(2)=10,
(1)确定函数f(x)的解析式;
(2)用定义证明f(x)在R上是增函数;
(3)若关于x的不等式f(x2-4)+f(kx+2k)<0在x∈(0,1)上恒成立,求k的取值范围.
解:(1)∵函数f(x)是奇函数
∴f(-x)=-f(x)即-ax
3+bx
2-cx=-ax
3-bx
2-cx
∴2bx=0
即b=0
∵
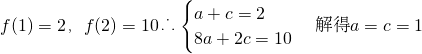
∴函数的解析式是f(x)=x
3+x 5分
(2)证明:设x
1,x
2是R上的任意两个不相等的实数,且x
1<x
2,
则△y=f(x
2)-f(x
1)=x
23+x
2-x
13-x
1=(x
2-x
1)(x
22+x
1x
2+x
12)+(x
2-x
1)
=

∵x
2-x
1>0,
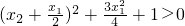
∴△y>0
∴函数f(x)在R上是增函数 (10分)
(3)∵f(x
2-4)+f(kx+2k)<0
∴f(x
2-4)<-f(kx+2k)=f(-kx-2k)
又因为f(x)是增函数,即x
2-4<-kx-2k
∴x
2+kx+2k-4<0在(0,1)上恒成立.(12分)
法(一)令g(x)=x
2+kx+2k-4,x∈(0,1)
则
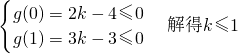
∴k的取值范围是(-∞,1]14分
法(二)上式可化为k(x+2)<4-x
2
∵x∈(0,1)即x+2>0∴
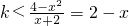
令U(x)=2-x,x∈(0,1)
∵U(x)=2-x在(0,1)上是减函数
∴U(x)<1即k≤1.(14分)
分析:(1)由“函数f(x)是奇函数”求或找到a,b,c的关系,再结合f(1)=2,f(2)=10求解.
(2)要求用定义,则先在给定的区间任取两个变量,且界定大小,再作差变形看符号.
(3)利用奇函数将“不等式f(x
2-4)+f(kx+2k)<0,在x∈(0,1)上恒成立”转化为“f(x
2-4)<f(-kx-2k)
在x∈(0,1)上恒成立”再由增函数的定义转化为“x
2+kx+2k-4<0在(0,1)上恒成立”求解.
点评:本题主要考查应用奇偶性来求函数解析式,应用单调性定义来证明函数的单调性,还考查了综合运用奇偶性和单调性来解不等式的能力.

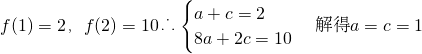

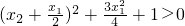 ∴△y>0
∴△y>0