火山喷发后,会在喷发区及周边地区地面上堆积起大量火山灰.在一次火山喷发停止后对地面火山灰的堆积量进行测量,设定距离喷口中心50m内的圆形区域为第1区,距离喷口中心50m至100m的圆环形区域为第2区,距离喷口中心100m至150m的圆环形区域为第3区,…,距离喷口中心50(n-1)m至50nm的圆环形区域为第n区….测得第1区火山灰堆积重量平均为1000kg/m2,第2区火山灰每平方米的平均重量比第1区减少2%,第3区比第2区又减少2%,…,依此类推(题中n∈N*,m表示长度单位米,kg表示重量单位千克).
(1)若第n区平均每平方米火山灰的堆积重量为an(kg),写出an的表达式;
(2)第几区内的火山灰的总重量最大?
解:(1)由题意,∵第1区火山灰堆积重量平均为1000kg/m
2,第2区火山灰每平方米的平均重量比第1区减少2%,第3区比第2区又减少2%,…,依此类推,
∴{a
n}组成以1000为首项,以1-0.02=0.98为公比的等比数列,…(4分)
所以a
n=1000×0.98
n-1.…(6分)
(2)设第n区的面积为b
nm
2,
则b
n=π•{(50n)
2-[50(n-1)]
2}=2500π•(2n-1),…(8分)
则第n区内火山灰的总重量为a
n•b
n=1000•2500π(2n-1)•(0.98)
n-1,…(10分)
设c
n=(2n-1)•(0.98)
n-1,若c
n最大,则有
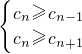
,
即
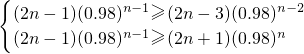
,解得

,
即49.5≤n≤50.5,…(13分)
所以n=50.即第50区内的火山灰总重量最大.…(14分)
分析:(1)由于第1区火山灰堆积重量平均为1000kg/m
2,第2区火山灰每平方米的平均重量比第1区减少2%,第3区比第2区又减少2%,…,依此类推,故{a
n}组成以1000为首项,以1-0.02=0.98为公比的等比数列,从而可求a
n的表达式;
(2)先求第n区的面积为b
nm
2,再求第n区内火山灰的总重量为a
n•b
n=1000•2500π(2n-1)•(0.98)
n-1,设c
n=(2n-1)•(0.98)
n-1,若c
n最大,则有
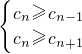
,从而可得n的值.
点评:本题的考点是函数模型的选择与应用,主要考查等比数列模型的构建即利用模型解决实际问题,关键是实际问题向数学问题的转化,同时考查解不等式.

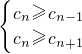 ,
,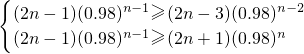 ,解得
,解得 ,
,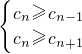 ,从而可得n的值.
,从而可得n的值.
