
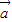 是平面内的单位向量,若向量
是平面内的单位向量,若向量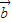 满足
满足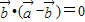 ,则
,则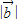 的取值范围是( )
的取值范围是( )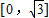
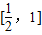
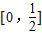
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案科目:高中数学 来源: 题型:
| 1 |
| 4 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
A.1 B.1-2i
C.2-i D.-i
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| 1 |
| 4 |
| 1 |
| 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:
(1)求p和q的值;
(2)试判断最少需要几秒钟,动点A、B能同时到达点D(1,2),并求在最短时间内它们同时到达点D的概率.
查看答案和解析>>
科目:高中数学 来源:2006年浙江省舟山中学高考数学三模试卷(理科)(解析版) 题型:解答题
 ,向上移动一个单位的概率是
,向上移动一个单位的概率是 ,向下移动一个单位的概率是p; 动点B向上、下、左、右移动一个单位的概率都是q.
,向下移动一个单位的概率是p; 动点B向上、下、左、右移动一个单位的概率都是q.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com