
【题目】在直角坐标系xOy中,圆C的参数方程 ![]() (φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(φ为参数),以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线l的极坐标方程是2ρsin(θ+ ![]() )=3
)=3 ![]() ,射线OM:θ=
,射线OM:θ= ![]() 与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
与圆C的交点为O、P,与直线l的交点为Q,求线段PQ的长.
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案科目:高中数学 来源: 题型:
【题目】设函数f(x)在R上存在导函数f′(x),对于任意的实数x,都有f(x)=4x2﹣f(﹣x),当x∈(﹣∞,0)时,f′(x)+ ![]() <4x,若f(m+1)≤f(﹣m)+4m+2,则实数m的取值范围是( )
<4x,若f(m+1)≤f(﹣m)+4m+2,则实数m的取值范围是( )
A.[﹣ ![]() ,+∞)
,+∞)
B.[﹣ ![]() ,+∞)
,+∞)
C.[﹣1,+∞)
D.[﹣2,+∞)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣ ![]() ﹣2alnx(a∈R) (Ⅰ)若函数f(x)在x=2时取极值,求实数a的值;
﹣2alnx(a∈R) (Ⅰ)若函数f(x)在x=2时取极值,求实数a的值;
(Ⅱ)若f(x)≥0对任意x∈[1,+∞)恒成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ex﹣ax﹣1﹣ ![]() ,x∈R.
,x∈R.
(Ⅰ)若a= ![]() ,求函数f(x)的单调区间;
,求函数f(x)的单调区间;
(Ⅱ)若对任意x≥0都有f(x)≥0恒成立,求实数a的取值范围;
(Ⅲ)设函数F(x)=f(x)+f(﹣x)+2+x2 , 求证:F(1)F(2)…F(n)>(en+1+2) ![]() (n∈N*).
(n∈N*).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】中国古代数学著作《孙子算经》中有这样一道算术题:“今有物不知其数,三三数之余二,五五数之余三,问物几何?”人们把此类题目称为“中国剩余定理”,若正整数N除以正整数m后的余数为n,则记为N=n(modm),例如11=2(mod3).现将该问题以程序框图的算法给出,执行该程序框图,则输出的n等于( ) 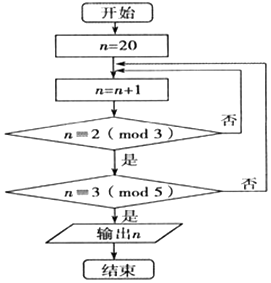
A.21
B.22
C.23
D.24
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某高中毕业学年,在高校自主招生期间,把学生的平时成绩按“百分制”折算,排出前n名学生,并对这n名学生按成绩分组,第一组[75,80),第二组[80,85),第三组[85,90),第四组[90,95),第五组[95,100],如图为频率分布直方图的一部分,其中第五组、第一组、第四组、第二组、第三组的人数依次成等差数列,且第四组的人数为60.
(Ⅰ)请在图中补全频率分布直方图;
(Ⅱ)若Q大学决定在成绩高的第3,4,5组中用分层抽样的方法抽取6名学生进行面试.
①若Q大学本次面试中有B、C、D三位考官,规定获得两位考官的认可即面试成功,且面试结果相互独立,已知甲同学已经被抽中,并且通过这三位考官面试的概率依次为 ![]() 、
、 ![]() ,
, ![]() ,求甲同学面试成功的概率;
,求甲同学面试成功的概率;
②若Q大学决定在这6名学生中随机抽取3名学生接受考官B的面试,第3组中有ξ名学生被考官B面试,求ξ的分布列和数学期望.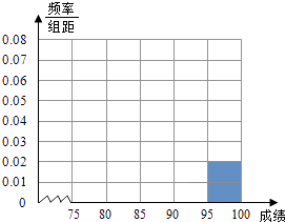
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知F为双曲线C: ![]() (a>0,b>0)的右焦点,l1 , l2为C的两条渐近线,点A在l1上,且FA⊥l1 , 点B在l2上,且FB∥l1 , 若
(a>0,b>0)的右焦点,l1 , l2为C的两条渐近线,点A在l1上,且FA⊥l1 , 点B在l2上,且FB∥l1 , 若 ![]() ,则双曲线C的离心率为( )
,则双曲线C的离心率为( )
A.![]()
B.![]()
C.![]() 或
或 ![]()
D.![]() 或
或 ![]()
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com