
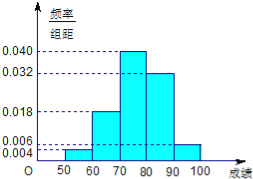
����Ŀ��ij��50��ѧ����һ����ѧ�����У��ɼ�ȫ������50��100֮�䣬�����Խ�������·�ʽ�ֳ����飺��һ��[50��60�����ڶ���[60��70��������������[90��100].��ͼ��ʾ�ǰ��������鷽���õ���Ƶ�ʷֲ�ֱ��ͼ.
���������ɼ����ڻ����60��С��80����Ϊ�ϸ���ð��������ѧ�����гɼ��ϸ��������
�������Ӳ��Գɼ���[50��60����[90��100]�ڵ�����ѧ���������ȡ����ͬѧ��������Գɼ��ֱ�Ϊm��n�����¼���|m��n|��10������.
���𰸡�
��������
�����������I����ֱ��ͼ֪���ɼ���[60��80���ڵ�����Ϊ��50��10����0.18+0.040��=29.���Ըð��������ѧ�����гɼ��ϸ����29��.
��II����ֱ��ͼ֪���ɼ���[50��60���ڵ�����Ϊ��50��10��0.004=2��
��ɼ�Ϊx��y
�ɼ���[90��100]������Ϊ50��10��0.006=3����ɼ�Ϊa��b��c��
��m��n��[50��60��ʱ��ֻ��xyһ�������
��m��n��[90��100]ʱ����ab��bc��ac���������
��m��n�ֱ���[50��60����[90��100]��ʱ����
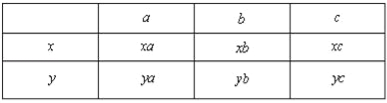
����6����������Ի����¼�����Ϊ10�֣�
�¼���|m��n|��10���������Ļ����¼�������6��
��![]() .
.



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪Բ![]() ������
������![]() ��Բ
��Բ![]() ��Բ����Բ
��Բ����Բ![]() ���ڲ�����ֱ��
���ڲ�����ֱ��![]() ��Բ
��Բ![]() ���صõ��ҳ�Ϊ
���صõ��ҳ�Ϊ![]() .��
.��![]() ΪԲ
ΪԲ![]() ������
������![]() ������һ�㣬ֱ��
������һ�㣬ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() ��ֱ��
��ֱ��![]() ��
��![]() �ύ�ڵ�
�ύ�ڵ�![]() .
.
��1����Բ![]() �ķ�����
�ķ�����
��2����֤:![]() Ϊ��ֵ��
Ϊ��ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪��Բ![]() ��Բ
��Բ![]() ���У�����Բ
���У�����Բ![]() �����У���Բ��
�����У���Բ��![]() �Ĺ켣Ϊ����
�Ĺ켣Ϊ����![]() ����
����![]() ����
Ϊ����![]() �ϵ�һ������
�ϵ�һ������![]() ���ϵĶ��㣬
���ϵĶ��㣬![]() Ϊ����ԭ�㣬����
Ϊ����ԭ�㣬����![]() ��
��![]() ��ƽ���߽�����
��ƽ���߽�����![]() ��
��![]() ������ͬ�ĵ㣮
������ͬ�ĵ㣮
��1��������![]() �ķ��̣�
�ķ��̣�
��2����̽��![]() ��
��![]() �ı�ֵ�ܷ�Ϊһ�����������ܣ������������������ܣ���˵�����ɣ�
�ı�ֵ�ܷ�Ϊһ�����������ܣ������������������ܣ���˵�����ɣ�
��3����![]() �����Ϊ
�����Ϊ![]() ��
��![]() �����Ϊ
�����Ϊ![]() ����
����![]() ����
����![]() �����ֵ��
�����ֵ��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪������![]() �Ķ���������ԭ��
�Ķ���������ԭ��![]() ���Գ���Ϊ
���Գ���Ϊ![]() �ᣬ����Ϊ
�ᣬ����Ϊ![]() ����������һ��
����������һ��![]() �ĺ�����Ϊ2����
�ĺ�����Ϊ2����![]() .
.
��1���������ߵķ��̣�
��2������![]() ��ֱ��
��ֱ��![]() ����������
����������![]() ���㣬��֤��
���㣬��֤��![]() .
.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ����������![]() �У���
�У���![]() Ϊ���Σ�
Ϊ���Σ�![]() Ϊ
Ϊ![]() ���е㣬
���е㣬![]() ��
��![]() ���ڵ�
���ڵ�![]() .
.
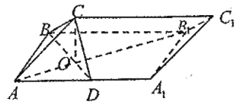
������֤����![]() ��
��
��������![]() ����BC��ƽ��ACD���ɽǵ�����ֵ.
����BC��ƽ��ACD���ɽǵ�����ֵ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ���й���������ְҵ�����ܾ��������߳���ʤ�ƣ�����ʤ�ij���ʤ���������ܾ����ļ��������У���ÿһ�������ӻ�ʤ�ĸ���Ϊ![]() ���Ҷӻ�ʤ�ĸ���Ϊ
���Ҷӻ�ʤ�ĸ���Ϊ![]() ������ÿ�������Ľ��������������������������Ҷ���2:0��ʱ���ȣ�
������ÿ�������Ľ��������������������������Ҷ���2:0��ʱ���ȣ�
��1����ӻ����α���ʤ���ĸ��ʣ�
��2�����������ʱ���ӱ����ij���Ϊ�������![]() �����������
�����������![]() �ķֲ��к���ѧ����
�ķֲ��к���ѧ����![]() ��
��
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����֪����![]() .
.
��1����![]() �Ǻ���
�Ǻ���![]() �ļ�ֵ�㣬��ʵ��
�ļ�ֵ�㣬��ʵ��![]() ��ֵ�����۵ĵ�����
��ֵ�����۵ĵ�����![]() ��
��
��2����![]() �Ǻ���
�Ǻ���![]() �ļ�ֵ�㣬��
�ļ�ֵ�㣬��![]() ���������ʵ��
���������ʵ��![]() ��ȡֵ��Χ��ע����֪����
��ȡֵ��Χ��ע����֪����![]() ����
����![]() ��.
��.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ����ͼ������![]() �У�
�У�![]() ƽ��
ƽ��![]() ���ı���
���ı���![]() ��ֱ�����Σ�����
��ֱ�����Σ�����![]() ��
��![]() .
.![]() ��
��![]() .
.
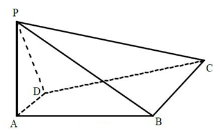
��1��������ֱ��![]() ��
��![]() ���ɽǵĴ�С��
���ɽǵĴ�С��
��2����ƽ��![]() ����һ������
����һ������![]() ������
������![]() ���������ϵ���һ����
���������ϵ���һ����![]() ������
������![]() ��
��![]() ���ɽǵĴ�Сǡ����
���ɽǵĴ�Сǡ����![]() ��
��![]() ���ɽ�.���ж�����
���ɽ�.���ж�����![]() ����״��˵�����ɣ�
����״��˵�����ɣ�
��3����ƽ��![]() �ڣ����
�ڣ����![]() �ǣ�2�����е�����
�ǣ�2�����е�����![]() ��ֱ������
��ֱ������![]() �ڲ��������߽磩��һ������
�ڲ��������߽磩��һ������![]() �ϵĶ��㣬����
�ϵĶ��㣬����![]() Ϊ����
����![]() ��
��![]() �Ľ���.��
�Ľ���.��![]() ΪԲ�ģ�
ΪԲ�ģ�![]() Ϊ�뾶
Ϊ�뾶![]() ��Բ�ֱ������εı�
��Բ�ֱ������εı�![]() ��
��![]() ����
����![]() ��
��![]() ����.��
����.��![]() �������߶�
�������߶�![]() ���˶�ʱ������Բ�뾶
���˶�ʱ������Բ�뾶![]() �ķ�Χ��
�ķ�Χ��![]() �ķ�Χ.
�ķ�Χ.
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�
����Ŀ��ij����Ҫ�������̡��˾ӵĹ��ʻ��³ǣ��ó��еĶ��������������ֱ�����8�����ң��ֶ����������16�����ҽ����������ۺϵ÷�����羥Ҷͼ��ʾ.

��1�����ݾ�Ҷͼ�ж��ĸ����ҵ�ƽ���ֽϸߣ�
��2���涨85�����ϣ���85�֣�Ϊ���㳧�ң����Ӹ����������ѡһ�����㳧�ң���÷ֲ�����5�ֵĸ���.
�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com