
如图,正四棱柱 中,底面边长为2,侧棱长为3,E为BC的中点,F、G分别为
中,底面边长为2,侧棱长为3,E为BC的中点,F、G分别为 、
、 上的点,且CF=2GD=2.求:
上的点,且CF=2GD=2.求:

(1) 到面EFG的距离;
到面EFG的距离;
(2)DA与面EFG所成的角的正弦值;
(3)在直线 上是否存在点P,使得DP//面EFG?,若存在,找出点P的位置,若不存在,试说明理由。
上是否存在点P,使得DP//面EFG?,若存在,找出点P的位置,若不存在,试说明理由。
1) (2)
(2)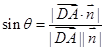 =
=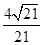 (3)DP//面EFG
(3)DP//面EFG
【解析】本试题主要是考查了空间几何体中点到面的距离,以及线面角的求解,和线面平行的判定的综合运用。
(1)合理的建立空间直角坐标系,利用向量在法向量上的投影得到点C‘到面EFG的距离;
(2)而对于线面角,DA与面EFG所成的角的正弦值则可以利用斜向量与法向量的关系,运用数量积的夹角公式得到。
(3)假设在直线BB’上是否存在点P,使得DP//面EFG,根据假设推理论证得到点P的坐标。解:如图,以D为原点建立空间直角坐标系
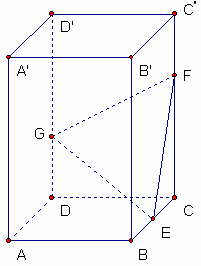
则E(1,2,0),F(0,2,2),G(0,0,1)∴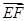 =(-1,0,2),
=(-1,0,2),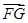 =(0,-2,-1),
=(0,-2,-1),
设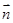 =(x,y,z)为面EFG的法向量,则
=(x,y,z)为面EFG的法向量,则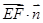 =0,
=0,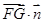 =0,
=0,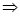 x=2z,z=-2y,取y=1,
x=2z,z=-2y,取y=1,
得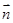 =(-4,1,-2)
=(-4,1,-2)
(1)∵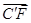 =(0,0,-1),∴C’到面EFG的距离为
=(0,0,-1),∴C’到面EFG的距离为
(2)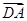 =(2,0,0),设DA与面EFG所成的角为θ,则
=(2,0,0),设DA与面EFG所成的角为θ,则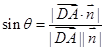 =
=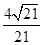
(3)存在点P,在B点下方且BP=3,此时P(2,2,-3)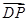 =(2,2,-3),∴
=(2,2,-3),∴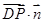 =0,∴DP//面EFG
=0,∴DP//面EFG


科目:高中数学 来源: 题型:
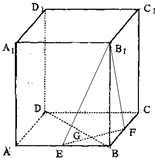 如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2
如图,正四棱柱ABCD-A1B1C1D1中,底面边长为2| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
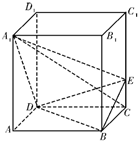 (2012•湖南模拟)如图,正四棱柱ABCD-A1B1C1D1(即底面为正方形的直四棱柱)中,AA1=2AB=4,点 E 在 CC1 上且 C1E=3EC.
(2012•湖南模拟)如图,正四棱柱ABCD-A1B1C1D1(即底面为正方形的直四棱柱)中,AA1=2AB=4,点 E 在 CC1 上且 C1E=3EC.查看答案和解析>>
科目:高中数学 来源:2013届北京市高二第一学期期中考试理科数学试卷 题型:解答题
如图,正四棱柱 中,
中, 的中点,
的中点, 为下底面正方形的中心,
为下底面正方形的中心,
(1)求证: ;
;
(2)求异面直线 所成角的余弦值;
所成角的余弦值;
(3)求二面角 的余弦值.
的余弦值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com