
(1)求A、C两个救援中心的距离;
(2)求在A处发现P的方向角.
解:(1)以AB中点为坐标原点,AB所在直线为x轴建立平面直角坐标系,则A(-3,0),B(3,0),C(5,23),则|AC|=![]() km=2
km=2![]() km,则A、C两个救援中心的距离为2
km,则A、C两个救援中心的距离为2![]() km.
km.

(2)∵|PC|=|PB|,∴P在BC线段的垂直平分线上.
又∵|PB|-|PA|=4,∴P在以A、B为焦点的双曲线的左支上且|AB|=6.
∴双曲线方程为![]() -
-![]() =1(x<0),BC的垂直平分线的方程为x+3y-7=0,联立两方程解得x=-8,
=1(x<0),BC的垂直平分线的方程为x+3y-7=0,联立两方程解得x=-8,
∴P(-8,5![]() ),kPA=tan∠PAB=-
),kPA=tan∠PAB=-![]() .
.
∴∠PAB=120°.∴P点在A点的北偏西30°处.
点评:实际问题有明显的几何意义,可以考虑用解析法建立适当的坐标系,构造曲线方程,利用曲线的性质来求解.


科目:高中数学 来源: 题型:
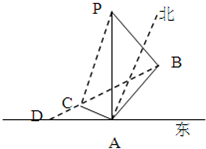 “神州”号飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回舱预计到达的区域安排了同一条直线上的三个救援中心(记为B,C,D).当返回舱距地面1万米的P点时(假定以后垂直下落,并在A点着陆),C救援中心测得飞船位于其南偏东60°方向,仰角为60°,B救援中心测得飞船位于其南偏西30°方向,仰角为30°.D救援中心测得着陆点A位于其正东方向.
“神州”号飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回舱预计到达的区域安排了同一条直线上的三个救援中心(记为B,C,D).当返回舱距地面1万米的P点时(假定以后垂直下落,并在A点着陆),C救援中心测得飞船位于其南偏东60°方向,仰角为60°,B救援中心测得飞船位于其南偏西30°方向,仰角为30°.D救援中心测得着陆点A位于其正东方向.查看答案和解析>>
科目:高中数学 来源: 题型:
(本小题满分12分)
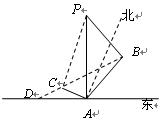
“神州”号飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回舱预![]() 计到达的区域安排了同一条直线上的三个救援中心(记为
计到达的区域安排了同一条直线上的三个救援中心(记为![]() ).当返回舱距地面1万米的
).当返回舱距地面1万米的![]() 点时(假定以后垂直下落,并在
点时(假定以后垂直下落,并在![]() 点着陆),
点着陆),![]() 救援中心测得飞船位于其南偏东
救援中心测得飞船位于其南偏东![]() 方向,仰角为
方向,仰角为![]() ,
,![]() 救援中心测得飞船位于其南偏西
救援中心测得飞船位于其南偏西![]() 方向,仰角为
方向,仰角为![]() .
.![]() 救援中心测得着陆点
救援中心测得着陆点![]() 位于其正东方向.
位于其正东方向.
(1)求![]()
![]() 两救援中心间的距离;
两救援中心间的距离;
(2)![]() 救援中心与着陆点
救援中心与着陆点![]() 间的距离.
间的距离.
查看答案和解析>>
科目:高中数学 来源:黑龙江省哈尔滨市第六中学2010届高三一模数学(理)试题 题型:解答题
(本小题满分12分)
“神州”号飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回舱预 计到达的区域安排了同一条直线上的三个救援中心(记为
计到达的区域安排了同一条直线上的三个救援中心(记为 ).当返回舱距地面1万米的
).当返回舱距地面1万米的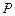 点时(假定以后垂直下落,并在
点时(假定以后垂直下落,并在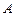 点着陆),
点着陆), 救援中心测得飞船位于其南偏东
救援中心测得飞船位于其南偏东 方向,仰角为
方向,仰角为 ,
,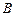 救援中心测得飞船位于其南偏西
救援中心测得飞船位于其南偏西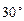 方向,仰角为
方向,仰角为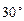 .
.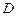 救援中心测得着陆点
救援中心测得着陆点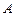 位于其正东方向.
位于其正东方向.
(1)求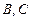
 两救援中心间的距离;
两救援中心间的距离;
(2)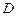 救援中心与着陆点
救援中心与着陆点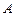 间的距离.
间的距离.
查看答案和解析>>
科目:高中数学 来源:黑龙江省哈尔滨市2010届高三一模数学(理)试题 题型:解答题
(本小题满分12分)
“神州”号飞船返回舱顺利到达地球后,为了及时将航天员救出,地面指挥中心在返回舱预计到达的区域安排了同一条直线上的三个救援中心(记为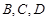 ).当返回舱距地面1万米的
).当返回舱距地面1万米的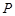 点时(假定以后垂直下落,并在
点时(假定以后垂直下落,并在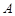 点着陆),
点着陆),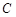 救援中心测得飞船位于其南偏东
救援中心测得飞船位于其南偏东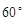 方向,仰角为
方向,仰角为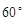 ,
,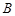 救援中心测得飞船位于其南偏西
救援中心测得飞船位于其南偏西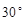 方向,仰角为
方向,仰角为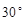 .
. 救援中心测得着陆点
救援中心测得着陆点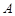 位于其正东方向.
位于其正东方向.
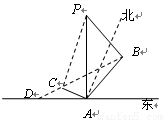
(1)求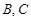 两救援中心间的距离;
两救援中心间的距离;
(2) 救援中心与着陆点
救援中心与着陆点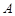 间的距离.
间的距离.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com