(1) f (-1) = -f (1) = 0,又f (x) 在 (0,+¥) 上是增函数,
∴ f (x) 在 (-¥,0) 上也是增函数,
∴ 由 f (x) < 0得x < -1或0 < x < 1.
(2) N =" {m" | f [g(q)] < 0} =" {m" | g(q) < -1或0 < g(q) < 1},
M∩N =" {m" | g(q) < -1}……………3分
由g(q) < -1得 sin
2q+ m cos q-2m < -1 Þ cos
2q-m cos q + 2m-2 > 0 恒成立
Þ(cos
2q-m cos q + 2m-2)
min > 0
然后换元构造函数设t = cosq,h(t) = cos
2q-m cos q + 2m-2
= t
2-mt + 2m-2 ,
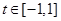
求其最值即可
(1)依题意,f (-1) = -f (1) = 0,又f (x) 在 (0,+¥) 上是增函数,
∴ f (x) 在 (-¥,0) 上也是增函数,
∴ 由 f (x) < 0得x < -1或0 < x < 1…………… 2分
(2)N =" {m" | f [g(q)] < 0} =" {m" | g(q) < -1或0 < g(q) < 1},
M∩N =" {m" | g(q) < -1}……………3分
由g(q) < -1得 sin
2q+ m cos q-2m < -1 Þ cos
2q-m cos q + 2m-2 > 0 恒成立
Þ(cos
2q-m cos q + 2m-2)
min > 0…………………4分
设t = cosq,h(t) = cos
2q-m cos q + 2m-2 = t
2-mt + 2m-2
= (t-
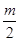
)
2-
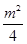
+ 2m-2,
∵ cosq∈[-1,1] Þt∈[-1,1],h(t) 的对称轴为 t =
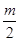
…5分
1°当
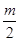
> 1,即 m > 2 时,h(t) 在 [-1,1] 为减函数
∴ h(t)
min =" h(1)" = m-1 > 0 Þm > 1 Þm > 2…………………7分
2°当 -1≤
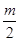
≤1,即 -2≤m≤2 时,
∴ h(t)
min = h(
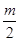
) = -
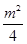
+ 2m-2 > 0 Þ4-2

< m < 4 + 2

Þ4-2

< m≤2…………9分
3°当
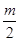
< -1,即 m < -2 时,h(t) 在 [-1,1] 为增函数
∴ h(t)
min = h(-1) = 3m-1 > 0 Þ m >
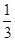
无解………………11分
综上,m > 4-2

Þ M∩N =" {m" | m > 4-2

}……………12分
另解:. 解:依题意,f (-1) = -f (1) = 0,又f (x) 在 (0,+¥) 上是增函数,
∴ f (x) 在 (-¥,0) 上也是增函数,
∴ 由 f (x) < 0得x < -1或0 < x < 1……………… 2分
∴ N =" {m" | f [g(q)] < 0} =" {m" | g(q) < -1或0 < g(q) < 1},
M∩N =" {m" | g(q) < -1}…………………3分
由g(q) < -1得 sin
2q+ m cos q-2m < -1 Þ cos
2q-m cos q + 2m-2 > 0 恒成立
Þ(cos
2q-m cos q + 2m-2)
min > 0
设t = cosq,h(t) = cos
2q-m cos q + 2m-2 = t
2-mt + 2m-2 = (t-
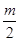
)
2-
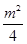
+ 2m-2
∵ cosq∈[-1,1] Þt∈[-1,1],h(t) 的对称轴为 t =
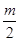
,△= m
2-8m + 8 …4分
1°当 △< 0,即 4-2

< m < 4 + 2

时,h(t) > 0 恒成立.…………………6分
2°当 △≥0,即 m≤4-2

或 m≥4 + 2

时,………7分
由 h(t) > 0 在 [-1,1] 上恒成立
∴
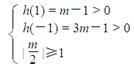
Þ m≥2 Þ m≥4 + 2

………………11分
综上,m > 4-2

Þ M∩N =" {m" | m > 4-2

}

 在
在 上有意义,且在
上有意义,且在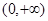 上是增函数,
上是增函数,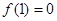
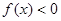 的实数
的实数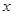 的取值范围;
的取值范围;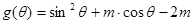 ,若集合
,若集合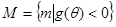 ,集合
,集合 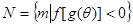 ,求
,求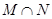
 }
}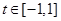 求其最值即可
求其最值即可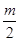 ) 2-
) 2-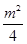 + 2m-2,
+ 2m-2, 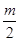 …5分
…5分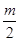 > 1,即 m > 2 时,h(t) 在 [-1,1] 为减函数
> 1,即 m > 2 时,h(t) 在 [-1,1] 为减函数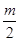 ≤1,即 -2≤m≤2 时,
≤1,即 -2≤m≤2 时, 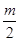 ) = -
) = -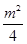 + 2m-2 > 0 Þ4-2
+ 2m-2 > 0 Þ4-2 < m < 4 + 2
< m < 4 + 2
 < m≤2…………9分
< m≤2…………9分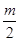 < -1,即 m < -2 时,h(t) 在 [-1,1] 为增函数
< -1,即 m < -2 时,h(t) 在 [-1,1] 为增函数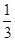 无解………………11分
无解………………11分 Þ M∩N =" {m" | m > 4-2
Þ M∩N =" {m" | m > 4-2 }……………12分
}……………12分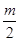 ) 2-
) 2-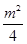 + 2m-2
+ 2m-2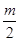 ,△= m 2-8m + 8 …4分
,△= m 2-8m + 8 …4分 < m < 4 + 2
< m < 4 + 2 时,h(t) > 0 恒成立.…………………6分
时,h(t) > 0 恒成立.…………………6分 或 m≥4 + 2
或 m≥4 + 2 时,………7分
时,………7分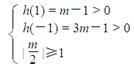 Þ m≥2 Þ m≥4 + 2
Þ m≥2 Þ m≥4 + 2 ………………11分
………………11分 Þ M∩N =" {m" | m > 4-2
Þ M∩N =" {m" | m > 4-2 }
}

 阅读快车系列答案
阅读快车系列答案