
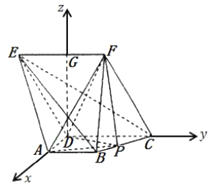
【题目】在五面体![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() ,平面
,平面![]() 平面
平面![]() ..
..
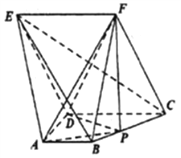
(1)证明:直线![]() 平面
平面![]() ;
;
(2)已知![]() 为棱
为棱![]() 上的点,试确定
上的点,试确定![]() 点位置,使二面角
点位置,使二面角![]() 的大小为
的大小为![]() .
.
【答案】(1)见解析;(2)![]() 点靠近
点靠近![]() 点的
点的![]() 的三等分点处.
的三等分点处.
【解析】试题分析:⑴证明一条直线垂直一个平面,只需要证明这条两个平面垂直,直线垂直两个平面的交线即可。证明![]() ,因为平面
,因为平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
, ![]() ,即可得到直线
,即可得到直线![]() 平面
平面![]()
⑵根据题意,取![]() 的中点
的中点![]() ,证明
,证明![]() ,
, ![]() ,
, ![]() 两两垂直,以
两两垂直,以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 为
为![]() ,
, ![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,进行计算,确定
,进行计算,确定![]() 点靠近
点靠近![]() 点的
点的![]() 的三等分点处
的三等分点处
解析:(1)证明:∵![]() ,∴
,∴![]() ,
,
∴四边形![]() 为菱形,∴
为菱形,∴![]() ,
,
∵平面![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∵![]() ,∴
,∴![]() 平面
平面![]() ,
,
∴![]() ,又∵
,又∵![]() ,
,
∴直线![]() 平面
平面![]() .
.
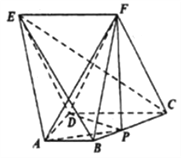
(2)∵![]() ,∴
,∴![]() 为正三角形,
为正三角形,
取![]() 的中点
的中点![]() ,连接
,连接![]() ,则
,则![]() ,∴
,∴![]() ,
,
∵平面![]() 平面
平面![]() ,
, ![]() 平面
平面![]() ,平面
,平面![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() ,
,
∵![]() ,∴
,∴![]() ,
, ![]() ,
, ![]() 两两垂直,
两两垂直,
以![]() 为原点,
为原点, ![]() ,
, ![]() ,
, ![]() 为
为![]() ,
, ![]() 轴,建立空间直角坐标系
轴,建立空间直角坐标系![]() ,如图,
,如图,
∵![]() ,
, ![]() ,
,
∴![]() ,
, ![]() .
.
由(1)知![]() 是平面
是平面![]() 的法向量,
的法向量,
∵![]() ,
, ![]() ,
,
设![]() ,则
,则![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
∵![]() ,
, ![]() ,∴
,∴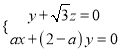 ,
,
令![]() ,则
,则![]() ,
, ![]() ,∴
,∴![]() ,
,
∵二面角![]() 为
为![]() ,
,
∴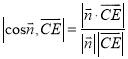
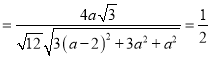 ,解得
,解得![]() .
.
∴![]() 点靠近
点靠近![]() 点的
点的![]() 的三等分点处.
的三等分点处.


 阅读快车系列答案
阅读快车系列答案科目:高中数学 来源: 题型:
【题目】在平面直角坐标系![]() 中,已知曲线
中,已知曲线![]() 与曲线
与曲线![]() ,(
,(![]() 为参数).以坐标原点为极点,
为参数).以坐标原点为极点,![]() 轴的正半轴为极轴建立极坐标系.
轴的正半轴为极轴建立极坐标系.
(1)写出曲线![]() ,
,![]() 的极坐标方程;
的极坐标方程;
(2)在极坐标系中,已知![]() 与
与![]() ,
,![]() 的公共点分别为
的公共点分别为![]() ,
,![]() ,
,![]() ,当
,当![]() 时,求
时,求![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某市房产中心数据研究显示,2018年该市新建住宅销售均价如下表.3月至7月房价上涨过快,为抑制房价过快上涨,政府从8月份开始出台了相关限购政策,10月份开始房价得到了很好的抑制.
均价(万元/ | 0.95 | 0.98 | 1.11 | 1.12 | 1.20 | 1.22 | 1.32 | 1.34 | 1.16 | 1.06 |
月份 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 |
(Ⅰ)请建立3月至7月线性回归模型(保留小数点后3位),并预测若政府不宏观调控,12月份该市新建住宅销售均价;
(Ⅱ)试用相关系数说明3月至7月各月均价![]() (万元/
(万元/![]() )与月份
)与月份![]() 之间可用线性回归模型(保留小数点后2位)
之间可用线性回归模型(保留小数点后2位)
参考数据:![]() ,
,![]() ,
,![]()
![]() ,
,![]() ,
,![]()
回归方程斜率和截距最小二乘法估计公式 ;
;
相关系数 .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的短轴长为2,直线
的短轴长为2,直线![]() 被椭圆截得的线段长为
被椭圆截得的线段长为![]() ,
,![]() 为坐标原点.
为坐标原点.
(1)求椭圆![]() 的方程;
的方程;
(2)是否存在过点![]() 且斜率为
且斜率为![]() 的直线
的直线![]() ,与椭圆交于
,与椭圆交于![]() 、
、![]() 两点时,作线段
两点时,作线段![]() 的垂直平分线分别交
的垂直平分线分别交![]() 轴、
轴、![]() 轴于
轴于![]() 、
、![]() ,垂足为
,垂足为![]() ,使得
,使得![]() 与
与![]() 的面积相等,若存在,试求出直线
的面积相等,若存在,试求出直线![]() 的方程,若不存在,请说明理由.
的方程,若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】2020年,新冠状肺炎疫情牵动每一个中国人的心,危难时刻众志成城,共克时艰,为疫区助力.福建省漳州市东山县共101个海鲜商家及个人为缓解武汉物质压力,募捐价值百万的海鲜输送武汉.东山岛,别称陵岛,形似蝴蝶亦称蝶岛,隶属于福建省漳州市东山县,是福建省第二大岛,中国第七大岛,介于厦门市和广东省汕头之间,东南是著名的闽南渔场和粤东渔场交汇处,因地理位置发展海产品养殖业具有得天独厚的优势.根据养殖规模与以往的养殖经验,某海鲜商家的海产品每只质量(克)在正常环境下服从正态分布![]() .
.
(1)随机购买10只该商家的海产品,求至少买到一只质量小于265克该海产品的概率;
(2)2020年该商家考虑增加先进养殖技术投入,该商家欲预测先进养殖技术投入为49千元时的年收益增量.现用以往的先进养殖技术投入![]() (千元)与年收益增量
(千元)与年收益增量![]() (千元).
(千元).![]() 的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线
的数据绘制散点图,由散点图的样本点分布,可以认为样本点集中在曲线![]() 的附近,且
的附近,且![]()
![]()
![]()
![]()
![]() ,
,![]()
![]() ,其中
,其中![]()
![]() .根据所给的统计量,求y关于x的回归方程,并预测先进养殖技术投入为49千元时的年收益增量.
.根据所给的统计量,求y关于x的回归方程,并预测先进养殖技术投入为49千元时的年收益增量.
附:若随机变量![]() ,则
,则![]()
![]() ;
;
对于一组数据![]()
![]()
![]()
![]() ,其回归线
,其回归线![]() 的斜率和截距的最小二乘估计分别为
的斜率和截距的最小二乘估计分别为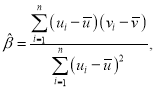
![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在直角坐标系![]() 中,以坐标原点为极点,
中,以坐标原点为极点,![]() 轴正半轴为极轴建立极坐标系,曲线
轴正半轴为极轴建立极坐标系,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数),直线
为参数),直线![]() 经过点
经过点![]() 且倾斜角为
且倾斜角为![]() .
.
(1)求曲线![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的参数方程;
的参数方程;
(2)已知直线![]() 与曲线
与曲线![]() 交于
交于![]() ,满足
,满足![]() 为
为![]() 的中点,求
的中点,求![]() .
.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com