
【题目】如图,几何体![]() 是四棱锥,△
是四棱锥,△![]() 为正三角形,
为正三角形,![]() .
.
(1)求证:![]() ;
;
(2)若∠![]() ,M为线段AE的中点,求证:
,M为线段AE的中点,求证:![]() ∥平面
∥平面![]() .
.
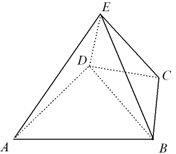
【答案】(1)见解析 (2) 见解析
【解析】本题考查直线与平面平行的判定,考查线面垂直的判定定理与面面平行的判定定理的应用,着重考查分析推理能力与表达、运算能力,属于中档题.
(1)设BD中点为O,连接OC,OE,则CO⊥BD,CE⊥BD,于是BD⊥平面OCE,从而BD⊥OE,即OE是BD的垂直平分线,问题解决;
(2)证法一:取AB中点N,连接MN,DN,MN,易证MN∥平面BEC,DN∥平面BEC,由面面平行的判定定理即可证得平面DMN∥平面BEC,又DM平面DMN,于是DM∥平面BEC;
证法二:延长AD,BC交于点F,连接EF,易证AB=![]() AF,D为线段AF的中点,连接DM,则DM∥EF,由线面平行的判定定理即可证得结论.
AF,D为线段AF的中点,连接DM,则DM∥EF,由线面平行的判定定理即可证得结论.
(I)设![]() 中点为O,连接OC,OE,则由
中点为O,连接OC,OE,则由![]() 知,
知,![]() ,…………2分
,…………2分
又已知![]() ,所以
,所以![]() 平面OCE. …………4分
平面OCE. …………4分
所以![]() ,即OE是BD的垂直平分线,
,即OE是BD的垂直平分线,
所以![]() .…………6分
.…………6分
(II)取AB中点N,连接![]() ,
,
∵M是AE的中点,∴![]() ∥
∥![]() ,…………8分
,…………8分
∵△![]() 是等边三角形,∴
是等边三角形,∴![]() .
.
由∠BCD=120°知,∠CBD=30°,所以∠ABC=60°+30°=90°,即![]() ,
,
所以ND∥BC,…………10分
所以平面MND∥平面BEC,故DM∥平面BEC. …………12分


科目:高中数学 来源: 题型:
【题目】给出下列五个命题:①“若![]() ,则
,则![]() 或
或![]() ”是假命题;②从正方体的面对角线中任取两条作为一对,其中所成角为
”是假命题;②从正方体的面对角线中任取两条作为一对,其中所成角为![]() 的有48对;③“
的有48对;③“ ![]() ”是方程
”是方程![]() 表示焦点在
表示焦点在![]() 轴上的双曲线的充分不必要条件;④点
轴上的双曲线的充分不必要条件;④点![]() 是曲线
是曲线![]() (
(![]() ,
, ![]() )上的动点,且满足
)上的动点,且满足![]() ,则
,则![]() 的取值范围是
的取值范围是![]() ;⑤若随机变量
;⑤若随机变量![]() 服从正态分布
服从正态分布![]() ,且
,且![]() ,则
,则![]() .其中正确命题的序号是__________(请把正确命题的序号填在横线上).
.其中正确命题的序号是__________(请把正确命题的序号填在横线上).
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】若函数![]() 的最小正周期为
的最小正周期为![]() .
.
(1)求![]() 的值;
的值;
(2)将函数![]() 的图像向左平移
的图像向左平移![]() 个单位,再将得到的图像上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数
个单位,再将得到的图像上各点的横坐标伸长到原来的4倍,纵坐标不变,得到函数![]() 的图像,求函数
的图像,求函数![]() 的单调递减区间.
的单调递减区间.
查看答案和解析>>
科目:高中数学 来源: 题型:
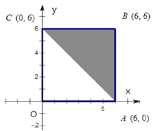
【题目】如图:区域A是正方形OABC(含边界),区域B是三角形ABC(含边界)。
(Ⅰ)向区域A随机抛掷一粒黄豆,求黄豆落在区域B的概率;
(Ⅱ)若x,y分别表示甲、乙两人各掷一次骰子所得的点数,求点(x,y)落在区域B的概率;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l1:3x+2y﹣1=0和l2:5x+2y+1=0的交点为A
(1)若直线l3:(a2﹣1)x+ay﹣1=0与l1平行,求实数a的值;
(2)求经过点A,且在两坐标轴上截距相等的直线l的方程.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com