
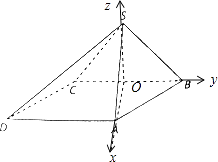
【题目】四棱锥S﹣ABCD中,底面ABCD为平行四边形,侧面SBC⊥面ABCD,已知∠ABC=45°,AB=2,BC=2 ![]() ,SB=SC=
,SB=SC= ![]() .
. 
(1)设平面SCD与平面SAB的交线为l,求证:l∥AB;
(2)求证:SA⊥BC;
(3)求直线SD与面SAB所成角的正弦值.
【答案】
(1)证明:∵底面ABCD为平行四边形,
∴AB∥CD,∵AB平面SCD,CD平面SCD,
∴AB∥平面SCD,又AB平面SAB,平面SCD∩平面SAB=l,
∴l∥AB.
(2)证明:取BC中点O,连接OS,OA.
∵OB= ![]() BC=
BC= ![]() ,AB=2,∠ABC=45°,
,AB=2,∠ABC=45°,
∴OA= ![]() =
= ![]() .
.
∴OA2+OB2=AB2,∴OA⊥BC.
∵SB=SC,O是BC的中点,∴OS⊥BC,
又SO平面SOA,OA平面SOA,SO∩OA=O,
∴BC⊥平面SOA,∵SA平面SOA,
∴BC⊥SA.
(3)解:∵SB=SC,O是BC中点,∴SO⊥BC.
∵侧面SBC⊥面ABCD,侧面SBC∩面ABCD=BC,
∴SO⊥平面ABCD.
以O为原点,以OA,OB,OS为坐标轴建立空间直角坐标系O﹣xyz,如图所示,
则A( ![]() ,0,0),B(0,
,0,0),B(0, ![]() ,0),S(0,0,1),D(
,0),S(0,0,1),D( ![]() ,﹣2
,﹣2 ![]() ,0),
,0),
∴ ![]() =(
=( ![]() ,﹣2
,﹣2 ![]() ,﹣1),
,﹣1), ![]() =(
=( ![]() ,0,﹣1),
,0,﹣1), ![]() =(
=( ![]() ,﹣
,﹣ ![]() ,0).
,0).
设平面SAB法向量为 ![]() =(x,y,z),则
=(x,y,z),则  ,
,
∴ ![]() .令x=1,则y=1,z=
.令x=1,则y=1,z= ![]() ,∴
,∴ ![]() =(1,1,
=(1,1, ![]() ).
).
∴cos< ![]() ,
, ![]() >=
>= 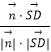 =
= ![]() =
= ![]() .
.
∴直线SD与面SAB所成角的正弦值为 ![]() .
.
【解析】
【考点精析】掌握棱锥的结构特征和空间角的异面直线所成的角是解答本题的根本,需要知道侧面、对角面都是三角形;平行于底面的截面与底面相似,其相似比等于顶点到截面距离与高的比的平方;已知![]() 为两异面直线,A,C与B,D分别是
为两异面直线,A,C与B,D分别是![]() 上的任意两点,
上的任意两点,![]() 所成的角为
所成的角为![]() ,则
,则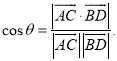 .
.


 期末冲刺100分创新金卷完全试卷系列答案
期末冲刺100分创新金卷完全试卷系列答案科目:高中数学 来源: 题型:
【题目】如图,已知PA垂直于矩形ABCD所在的平面,M、N分别为AB、PC的中点,且![]() .
.

(1)求证:![]() 平面PAD;
平面PAD;
(2)求证:![]() 面PCD;
面PCD;
(3)若![]() ,求二面角
,求二面角![]() 的正弦值.
的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=2x2+bx﹣alnx.
(1)当a=5,b=﹣1时,求f(x)的单调区间;
(2)若对任意b∈[﹣3,﹣2],都存在x∈(1,e2)(e为自然对数的底数),使得f(x)<0成立,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知定义在R上的函数f(x)和g(x)满足f(x)= ![]() e2x﹣2+x2﹣2f(0)x,且g′(x)+2g(x)<0,则下列不等式成立的是( )
e2x﹣2+x2﹣2f(0)x,且g′(x)+2g(x)<0,则下列不等式成立的是( )
A.f(2)g(2015)<g(2017)
B.f(2)g(2015)>g(2017)
C.g(2015)>f(2)g(2017)
D.g(2015)>f(2)g(2017)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设函数f(x)=x2﹣aln(x+2),g(x)=xex , 且f(x)存在两个极值点x1、x2 , 其中x1<x2 .
(1)求实数a的取值范围;
(2)求g(x1﹣x2)的最小值;
(3)证明不等式:f(x1)+x2>0.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2+10x+10y+34=0.
(Ⅰ)试写出圆C的圆心坐标和半径;
(Ⅱ)圆D的圆心在直线x=-5上,且与圆C相外切,被x轴截得的弦长为10,求圆D的方程;
(Ⅲ)过点P(0,2)的直线交(Ⅱ)中圆D于E,F两点,求弦EF的中点M的轨迹方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某学校为了解该校教师对教工食堂的满意度情况,随机访问了![]() 名教师.根据这
名教师.根据这![]() 名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为:
名教师对该食堂的评分,绘制频率分布直方图(如图所示),其中样本数据分组区间为: ![]() ,
, ![]() ,…,
,…, ![]() ,
, ![]() .
.
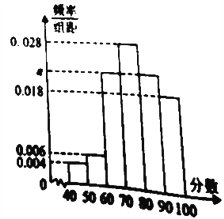
(1)求频率分布直方图中![]() 的值;
的值;
(2)从评分在![]() 的受访教师中,随机抽取2人,求此2人的评分都在
的受访教师中,随机抽取2人,求此2人的评分都在![]() 的概率.
的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com