
【题目】2016年备受瞩目的二十国集团领导人第十一次峰会于9月4~5日在杭州举办,杭州G20筹委会已经招募培训翻译联络员1000人、驾驶员2000人,为测试培训效果,采取分层抽样的方法从翻译联络员、驾驶员中共随机抽取60人,对其做G20峰会主题及相关服务职责进行测试,将其所得分数(分数都在60~100之间)制成频率分布直方图如下图所示,若得分在90分及其以上(含90分)者,则称其为“G20通”. 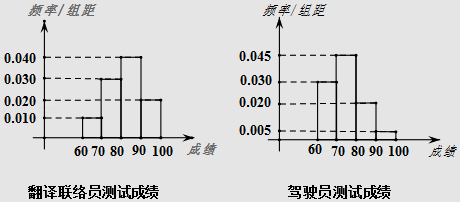
(Ⅰ)能否有90%的把握认为“G20通”与所从事工作(翻译联络员或驾驶员)有关?
(Ⅱ)从参加测试的成绩在80分以上(含80分)的驾驶员中随机抽取4人,4人中“G20通”的人数为随机变量X,求X的分布列与数学期望.
P(K2≥k0) | 0.10 | 0.05 | 0.010 | 0.001 |
k0 | 2.706 | 3.841 | 6.635 | 10.828 |
附参考公式与数据: ![]() .
.
【答案】解:(Ⅰ)由已知可得:翻译联络员得分在90分及其以上(含90分)者有0.02×10×1000=200人, 得分在90分及其以下者有1000﹣200=800人.
驾驶员得分在90分及其以上(含90分)者有0.005×10×2000=100人,得分在90分及其以下者有2000﹣200=1900人.
抽取翻译联络员= ![]() =20人,得分在90分及其以上(含90分)者有4人,得分在90分及其以下者有16人,
=20人,得分在90分及其以上(含90分)者有4人,得分在90分及其以下者有16人,
抽取驾驶员 ![]() ×60=40人,得分在90分及其以上(含90分)者有2人,得分在90分及其以下者有38人.
×60=40人,得分在90分及其以上(含90分)者有2人,得分在90分及其以下者有38人.
做出列联表:
90(含90)分以上 | 90分以下 | 合计 | |
翻译联络员 | 4 | 16 | 20 |
驾驶员 | 2 | 38 | 40 |
合计 | 6 | 54 | 60 |
由列联表中的数据,得到k2= ![]() =3.333>2.706.
=3.333>2.706.
因此,有90%的把握认为两者有关.
(Ⅱ)由图可知:参加测试的成绩在80分以上(含80分)的驾驶员中共有10人,其中在区间[80,90)的有8人,在区间[90,100]的有2人.
随机抽取4人,4人中“G20通”的人数为随机变量X=0,1,2.
P(X=k)= ![]() ,可得P(X=0)=
,可得P(X=0)= ![]() ,P(X=1)=
,P(X=1)= ![]() ,P(X=2)=
,P(X=2)= ![]() .
.
X | 0 | 1 | 2 |
P |
|
|
|
EX=0+ ![]() =
= ![]()
【解析】(Ⅰ)由已知可得:翻译联络员得分在90分及其以上(含90分)者有0.02×10×1000=200人,得分在90分及其以下者有1000﹣200=800人.驾驶员得分在90分及其以上(含90分)者有0.005×10×2000=100人,得分在90分及其以下者有2000﹣200=1900人.抽取翻译联络员= ![]() =20人,得分在90分及其以上(含90分)者有4人,得分在90分及其以下者有16人,抽取驾驶员
=20人,得分在90分及其以上(含90分)者有4人,得分在90分及其以下者有16人,抽取驾驶员 ![]() ×60=40人,得分在90分及其以上(含90分)者有2人,得分在90分及其以下者有38人.作出列联表:由列联表中的数据,得到k2=
×60=40人,得分在90分及其以上(含90分)者有2人,得分在90分及其以下者有38人.作出列联表:由列联表中的数据,得到k2= ![]() =3.333,即可得出结论.(Ⅱ)由图可知:参加测试的成绩在80分以上(含80分)的驾驶员中共有10人,其中在区间[80,90)的有8人,在区间[90,100]的有2人.随机抽取4人,4人中“G20通”的人数为随机变量X=0,1,2.P(X=k)=
=3.333,即可得出结论.(Ⅱ)由图可知:参加测试的成绩在80分以上(含80分)的驾驶员中共有10人,其中在区间[80,90)的有8人,在区间[90,100]的有2人.随机抽取4人,4人中“G20通”的人数为随机变量X=0,1,2.P(X=k)= ![]() ,即可得出.
,即可得出.


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】如图,已知直三棱柱ABC﹣A1B1C1的底面是边长为4的正三角形,B,E,F分别是AA1 , CC1的中点,且BE⊥B1F. 
(1)求证:B1F⊥EC1;
(2)求二面角C1﹣BE﹣C的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某单位员工![]() 人参加“学雷锋”志愿活动,按年龄分组:第
人参加“学雷锋”志愿活动,按年龄分组:第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,第
,第![]() 组
组![]() ,得到的频率分布直方图如图所示.
,得到的频率分布直方图如图所示.

(1)下表是年龄的频率分布表,求正整数![]() 的值;
的值;
区间 |
|
|
|
|
|
人数 |
|
|
|
|
|
(2)现在要从年龄较小的第![]() 组中用分层抽样的方法抽取
组中用分层抽样的方法抽取![]() 人,年龄在第
人,年龄在第![]() 组抽取的员工的人数分别是多少?
组抽取的员工的人数分别是多少?
(3)在(2)的前提下,从这![]() 人中随机抽取
人中随机抽取![]() 人参加社区宣传交流活动,求至少有
人参加社区宣传交流活动,求至少有![]() 人年龄在第
人年龄在第![]() 组的概率.
组的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)讨论函数y=f(x)在∈(m,+∞)上的单调性;
(2)若![]() ,则当x∈[m,m+1]时,函数y= f(x)的图象是否总在函数
,则当x∈[m,m+1]时,函数y= f(x)的图象是否总在函数![]() 图象上方?请写出判断过程.
图象上方?请写出判断过程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在平面直角坐标系中,以坐标原点为极点,x轴的非负半轴为极轴,长度单位相同,建立极坐标系,已知圆A的参数方程为 ![]() (其中θ为参数),圆B的极坐标方程为ρ=2sinθ.
(其中θ为参数),圆B的极坐标方程为ρ=2sinθ.
(Ⅰ)分别写出圆A与圆B的直角坐标方程;
(Ⅱ)判断两圆的位置关系,若两圆相交,求其公共弦长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知三点A(1,﹣1),B(3,0),C(2,1),P为平面ABC上的一点, ![]() =λ
=λ ![]() +μ
+μ ![]() ,且
,且 ![]()
![]() =0,
=0, ![]()
![]() =3.
=3.
(1)求 ![]()
![]() ;
;
(2)求λ+μ 的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某工厂第一季度某产品月生产量分别为10万件,12万件,13万件,为了预测以后每个月的产量,以这3个月的产量为依据,用一个函数模拟该产品的月产量y (单位:万件)与月份x 的关系.模拟函数1:y=ax+ ![]() +c
+c
;模拟函数2:y=mnx+s.
(1)已知4月份的产量为13.7 万件,问选用哪个函数作为模拟函数好?
(2)受工厂设备的影响,全年的每月产量都不超过15万件,请选用合适的模拟函数预测6月份的产量.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某校对高三年级的学生进行体检,现将高三男生体重(单位:kg)的数据进行整理后分为五组,并绘制出频率分布直方图(如图所示).根据一般标准,高三男生的体重超过65 kg属于偏胖,低于55 kg属于偏瘦.已知图中从左到右第一、第三、第四、第五小组的频率分别为0.25,0.20,0.10,0.05,第二小组的频数为400,则该校高三年级男生的总数和体重正常的频率分别为( )

A. 1000,0.50 B. 800,0.50
C. 800,0.60 D. 1000,0.60
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出两个命题:
命题甲:关于x的不等式x2+(a﹣1)x+a2≤0的解集为;
命题乙:函数y=(2a2﹣a)x为增函数.
(1)甲、乙至少有一个是真命题;
(2)甲、乙有且只有一个是真命题;
分别求出符合(1)(2)的实数a的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com