
【题目】某校为了探索一种新的教学模式,进行了一项课题实验,甲班为实验班,乙班为对比班,甲乙两班的人数均为50人,一年后对两班进行测试,测试成绩的分组区间为![]() 80,90
80,90![]() 、
、![]() 90,100
90,100![]() 、
、![]() 100,110
100,110![]() 、
、![]() 110,120
110,120![]() 、
、![]() 120,130
120,130![]() ,由此得到两个班测试成绩的频率分布直方图:
,由此得到两个班测试成绩的频率分布直方图:
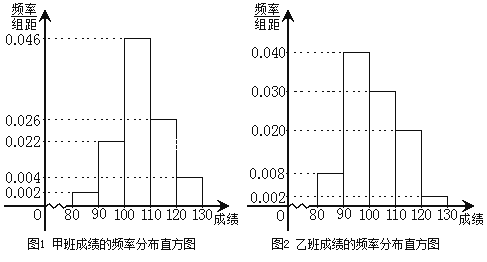
(1)完成下面2×2列联表,你能有97.5![]() 的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
的把握认为“这两个班在这次测试中成绩的差异与实施课题实验有关”吗?并说明理由;
成绩小于100分 | 成绩不小于100分 | 合计 | |
甲班 |
|
| 50 |
乙班 |
|
| 50 |
合计 |
|
| 100 |
(2)根据所给数据可估计在这次测试中,甲班的平均分是105.8,请你估计乙班的平均分,并计算两班平均分相差几分?
附:
![]() ,其中
,其中![]()
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5. 024 | 6.635 | 7.879 | 10.828 |
科目:高中数学 来源: 题型:
【题目】一个多面体的直观图及三视图如图所示:(其中M,N分别是AF,BC的中点). 
(1)求证:MN∥平面CDEF;
(2)求多面体A﹣CDEF的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f (x)=a lnx+![]() +x (a≠0).
+x (a≠0).
(1)若曲线y=f (x)在点(1,f (1))处的切线与直线x-2y=0垂直,求实数a的值;
(2)讨论函数f (x)的单调性.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=4cosxsin(x+![]() )-1.
)-1.
(1)求f(x)的最小正周期和单调递减区间;
(2)将y=f(x)图象上所有的点向右平行移动![]() 个单位长度,得到y=g(x)的图象.若g(x)在(0,m)内是单调函数,求实数m的最大值.
个单位长度,得到y=g(x)的图象.若g(x)在(0,m)内是单调函数,求实数m的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=x﹣1+ ![]() (a∈R).
(a∈R).
(1)若曲线y=f(x)在点(1,f(1))处的切线平行于x轴,求a的值;
(2)求函数f(x)的极值;
(3)当a=1时,若直线l:y=kx﹣1与曲线y=f(x)没有公共点,求k的最大值.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com