
【题目】阅读下列材料:
北京市正围绕着“政治中心、文化中心、国际交往中心、科技创新中心”的定位,深入实施“人文北京、科技北京、绿色北京”的发展战略.“十二五”期间,北京市文化创意产业展现了良好的发展基础和巨大的发展潜力,已经成为首都经济增长的支柱产业.
2011年,北京市文化创意产业实现增加值1938.6亿元,占地区生产总值的12.2%.2012年,北京市文化创意产业继续呈现平稳发展态势,实现产业增加值2189.2亿元,占地区生产总值的12.3%,是第三产业中仅次于金融业、批发和零售业的第三大支柱产业.2013年,北京市文化产业实现增加值2406.7亿元,比上年增长9.1%,文化创意产业作为北京市支柱产业已经排到了第二位.2014年,北京市文化创意产业实现增加值2749.3亿元,占地区生产总值的13.1%,创历史新高,2015年,北京市文化创意产业发展总体平稳,实现产业增加值3072.3亿元,占地区生产总值的13.4%.
根据以上材料解答下列问题:
(1)用折线图将2011﹣2015年北京市文化创意产业实现增加值表示出来,并在图中标明相应数据;
(2)根据绘制的折线图中提供的信息,预估2016年北京市文化创意产业实现增加值约亿元,你的预估理由 .
【答案】
(1)
解:(1)2011﹣2015年北京市文化创意产业实现增加值如图所示,
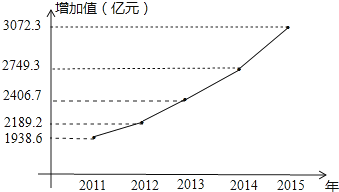
(2)3471.7;用近3年的平均增长率估计2016年的增长率
【解析】(2)解:设2013到2015的平均增长率为x,
则2406.7(1+x)2=3072.3,
解得x≈13%,
用近3年的平均增长率估计2016年的增长率,
∴2016年的增长率为3072.3×(1+13%)≈3471.7亿元.
故答案分别为3471.7,用近3年的平均增长率估计2016年的增长率.
本题考查折线图、样本估计总体的思想,解题的关键是用近3年的平均增长率估计2016年的增长率,属于中考常考题型.(1)画出2011﹣2015的北京市文化创意产业实现增加值折线图即可.(2)设2013到2015的平均增长率为x,列出方程求出x,用近3年的平均增长率估计2016年的增长率即可解决问题.


科目:高中数学 来源: 题型:
【题目】如图是将一正方体货物沿坡面AB装进汽车货厢的平面示意图.已知长方体货厢的高度BC为 ![]() 米,tanA=
米,tanA= ![]() ,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)
,现把图中的货物继续往前平移,当货物顶点D与C重合时,仍可把货物放平装进货厢,求BD的长.(结果保留根号)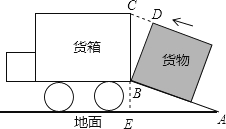
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知抛物线y=﹣ ![]() +bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).
+bx+c与y轴交于点C,与x轴的两个交点分别为A(﹣4,0),B(1,0).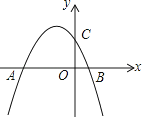
(1)求抛物线的解析式;
(2)已知点P在抛物线上,连接PC,PB,若△PBC是以BC为直角边的直角三角形,求点P的坐标;
(3)已知点E在x轴上,点F在抛物线上,是否存在以A,C,E,F为顶点的四边形是平行四边形?若存在,请直接写出点E的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知圆C:x2+y2-2x+4y-4=0,
(1)求圆C关于直线![]() 对称的圆的方程;
对称的圆的方程;
(2)问是否存在斜率为1的直线l,使l被圆C截得弦AB,且以AB为直径的圆经过点![]() ?若存在,求出直线l的方程;若不存在,说明理由.
?若存在,求出直线l的方程;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某养殖场需定期购买饲料,已知该场每天需要饲料200千克,每千克饲料的价格为1.8元,饲料的保管费与其他费用平均每千克每天0.03元,购买饲料每次支付运费300元.
(1)求该场多少天购买一次饲料才能使平均每天支付的总费用最少;
(2)若提供饲料的公司规定,当一次购买饲料不少于5吨时,其价格可享受八五折优惠(即原价为85%).问:该场是否应考虑利用此优惠条件?请说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知y是x的函数,自变量x的取值范围x>0,下表是y与x的几组对应值:
x | … | 1 | 2 | 3 | 5 | 7 | 9 | … |
y | … | 1.98 | 3.95 | 2.63 | 1.58 | 1.13 | 0.88 | … |
小腾根据学习函数的经验,利用上述表格所反映出的y与x之间的变化规律,对该函数的图象与性质进行了探究.
下面是小腾的探究过程,请补充完整:
(1)如图,在平面直角坐标系xOy中,描出了以上表格中各对对应值为坐标的点,根据描出的点,画出该函数的图象;
(2)根据画出的函数图象,写出:
①x=4对应的函数值y约为
②该函数的一条性质:
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知点![]() 的坐标为
的坐标为![]() ,圆
,圆![]() 的方程为
的方程为![]() ,动点
,动点![]() 在圆
在圆![]() 上运动,点
上运动,点![]() 为
为![]() 延长线上一点,且
延长线上一点,且![]() .
.
(1)求点![]() 的轨迹方程.
的轨迹方程.
(2)过点![]() 作圆
作圆![]() 的两条切线
的两条切线![]() ,
, ![]() ,分别与圆
,分别与圆![]() 相切于点
相切于点![]() ,
, ![]() ,求直线
,求直线![]() 的方程,并判断直线
的方程,并判断直线![]() 与点
与点![]() 所在曲线的位置关系.
所在曲线的位置关系.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(本小题满分10分)选修4—4:坐标系与参数方程
在直角坐标系xOy中,圆C的参数方程![]() 为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
为参数).以O为极点,x轴的非负半轴为极轴建立极坐标系.
(1)求圆C的极坐标方程;
(2)直线![]() 的极坐标方程是
的极坐标方程是![]() ,射线
,射线![]() 与圆C的交点为O、P,与直线
与圆C的交点为O、P,与直线![]() 的交点为Q,求线段PQ的长.
的交点为Q,求线段PQ的长.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】【2016高考北京文数】某市居民用水拟实行阶梯水价,每人月用水量中不超过w立方米的部分按4元/立方米收费,超出w立方米的部分按10元/立方米收费.从该市随机调查了10 000位居民,获得了他们某月的用水量数据,整理得到如下频率分布直方图:

(I)如果w为整数,那么根据此次调查,为使80%以上居民在该月的用水价格为4元/立方米,w至少定为多少?
(II)假设同组中的每个数据用该组区间的右端点值代替,当w=3时,估计该市居民该月的人均水费.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com