
ЁОЬтФПЁПФГЦѓвЕЩњВњвЛжжВњЦЗЃЌжЪСПВтЪдЗжЮЊЃКжИБъВЛаЁгк90ЮЊвЛЕШЦЗЃЌВЛаЁгк80аЁгк90ЮЊЖўЕШЦЗЃЌаЁгк80ЮЊШ§ЕШЦЗЃЌУПМўвЛЕШЦЗгЏРћ50дЊЃЌУПМўЖўЕШЦЗгЏРћ30дЊЃЌУПМўШ§ЕШЦЗПїЫ№10дЊ.ЯжЖдбЇЭНЙЄМзКЭе§ЪНЙЄШЫввЩњВњЕФВњЦЗИї100МўЕФМьВтНсЙћЭГМЦШчЯТЃК

ИљОнЩЯБэЭГМЦЕУЕНМзЁЂввЩњВњВњЦЗЕШМЖЕФЦЕТЪЗжБ№ЙРМЦЮЊЫћУЧЩњВњВњЦЗЕШМЖЕФИХТЪ.
ЃЈЂёЃЉЧѓГіМзЩњВњШ§ЕШЦЗЕФИХТЪЃЛ
ЃЈЂђЃЉЧѓГіввЩњВњвЛМўВњЦЗЃЌгЏРћВЛаЁгк30дЊЕФИХТЪЃЛ
ЃЈЂѓЃЉШєМзЁЂвввЛЬьЩњВњВњЦЗЗжБ№ЮЊ30МўКЭ40МўЃЌЙРМЦМзЁЂввСНШЫвЛЬьЙВЮЊЦѓвЕДДЪеЖрЩйдЊЃП
ЁОД№АИЁП(Ђё)![]() ЃЛ(Ђђ)
ЃЛ(Ђђ)![]() ЃЛ(Ђѓ)2000дЊ.
ЃЛ(Ђѓ)2000дЊ.
ЁОНтЮіЁП
ЪдЬтЗжЮіЃК
(Ђё)гЩЬтвтПЩЕУЃКМзЩњВњШ§ЕШЦЗЕФВтЪджИБъаЁгк80ЃЌОнДЫНсКЯЙХЕфИХаЭМЦЫуЙЋЪНПЩЕУ![]() .
.
(Ђђ)гЩЬтвтПЩЕУЃКввЩњВњвЛМўВњЦЗЕФВтЪджИБъВЛаЁгк80ЃЌОнДЫНсКЯЙХЕфИХаЭМЦЫуЙЋЪНПЩЕУ![]() .
.
(Ђѓ)гЩЬтвтНсКЯЙХЕфИХаЭМЦЫуЙЋЪНПЩЕУМзЩњВњШ§ЕШЦЗЃЌЖўЕШЦЗвЛЕШЦЗЕФМўЪ§ЮЊ6ЃЌ21,3ЃЌввЩњВњШ§ЕШЦЗЃЌЖўЕШЦЗвЛЕШЦЗЕФМўЪ§ЮЊ4,24,12ЃЌОнДЫЙРМЦПЩЕУМзЁЂввСНШЫвЛЬьЙВЮЊЦѓвЕДДЪе2000дЊ.
ЪдЬтНтЮіЃК
ЃЈЂёЃЉвРЬтвтЃЌМзЩњВњШ§ЕШЦЗЃЌМДЮЊВтЪджИБъаЁгк80ЃЌ
ЫљЧѓИХТЪЮЊЃК![]() .
.
ЃЈЂђЃЉвРЬтвтЃЌввЩњВњвЛМўВњЦЗЃЌгЏРћВЛаЁгк30дЊЃЌМДЮЊВтЪджИБъВЛаЁгк80ЃЌ
ЫљЧѓИХТЪЮЊЃК![]() .
.
ЃЈЂѓЃЉМзвЛЬьЩњВњ30МўВњЦЗЃЌЦфжаЃК
Ш§ЕШЦЗЕФМўЪ§ЮЊ![]() ЃЌ
ЃЌ
ЖўЕШЦЗЕФМўЪ§ЮЊ![]() ЃЌ
ЃЌ
вЛЕШЦЗЕФМўЪ§ЮЊ![]() ЃЛ
ЃЛ
вввЛЬьЩњВњ40МўВњЦЗЃЌЦфжаЃК
Ш§ЕШЦЗЕФМўЪ§ЮЊ![]() ЃЌ
ЃЌ
ЖўЕШЦЗЕФМўЪ§ЮЊ![]() ЃЌ
ЃЌ
вЛЕШЦЗЕФМўЪ§ЮЊ![]() .
.
дђ![]() .
.
ЁрЙРМЦМзЁЂввСНШЫвЛЬьЙВЮЊЦѓвЕДДЪе2000дЊ.


 дФЖСПьГЕЯЕСаД№АИ
дФЖСПьГЕЯЕСаД№АИ
| ФъМЖ | ИпжаПЮГЬ | ФъМЖ | ГѕжаПЮГЬ |
| ИпвЛ | ИпвЛУтЗбПЮГЬЭЦМіЃЁ | ГѕвЛ | ГѕвЛУтЗбПЮГЬЭЦМіЃЁ |
| ИпЖў | ИпЖўУтЗбПЮГЬЭЦМіЃЁ | ГѕЖў | ГѕЖўУтЗбПЮГЬЭЦМіЃЁ |
| ИпШ§ | ИпШ§УтЗбПЮГЬЭЦМіЃЁ | ГѕШ§ | ГѕШ§УтЗбПЮГЬЭЦМіЃЁ |
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПдкШчЭМЫљЪОЕФМИКЮЬхжаЃЌЫФБпаЮABCDЮЊе§ЗНаЮЃЌ![]() ЮЊжБНЧШ§НЧаЮЃЌ
ЮЊжБНЧШ§НЧаЮЃЌ![]() ЃЌЧв
ЃЌЧв![]() .
.

ЃЈ1ЃЉжЄУїЃКЦНУц![]() ЦНУц
ЦНУц![]() ЃЛ
ЃЛ
ЃЈ2ЃЉШєAB=2AEЃЌЧѓвьУцжБЯпBEгыACЫљГЩНЧЕФгрЯвжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЇаЃИпвЛФъМЖПЊЩш![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЁЂ
ЁЂ![]() ЮхУХбЁаоПЮЃЌУПЮЛЭЌбЇаыБЫДЫЖРСЂЕибЁШ§ПЮГЬЃЌЦфжаМзЭЌбЇБибЁ
ЮхУХбЁаоПЮЃЌУПЮЛЭЌбЇаыБЫДЫЖРСЂЕибЁШ§ПЮГЬЃЌЦфжаМзЭЌбЇБибЁ![]() ПЮГЬЃЌВЛбЁ
ПЮГЬЃЌВЛбЁ![]() ПЮГЬЃЌСэДгЦфгрПЮГЬжаЫцЛњШЮбЁСНУХПЮГЬЃЎввЁЂБћСНУћЭЌбЇДгЮхУХПЮГЬжаЫцЛњШЮбЁШ§УХПЮГЬЃЎ
ПЮГЬЃЌСэДгЦфгрПЮГЬжаЫцЛњШЮбЁСНУХПЮГЬЃЎввЁЂБћСНУћЭЌбЇДгЮхУХПЮГЬжаЫцЛњШЮбЁШ§УХПЮГЬЃЎ
ЃЈЂёЃЉЧѓМзЭЌбЇбЁжа![]() ПЮГЬЧвввЭЌбЇЮДбЁжа
ПЮГЬЧвввЭЌбЇЮДбЁжа![]() ПЮГЬЕФИХТЪЃЎ
ПЮГЬЕФИХТЪЃЎ
ЃЈЂђЃЉгУ![]() БэЪОМзЁЂввЁЂБћбЁжа
БэЪОМзЁЂввЁЂБћбЁжа![]() ПЮГЬЕФШЫЪ§жЎКЭЃЌЧѓ
ПЮГЬЕФШЫЪ§жЎКЭЃЌЧѓ![]() ЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ЕФЗжВМСаКЭЪ§бЇЦкЭћЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊгаЯоМЏ![]() . ШчЙћ
. ШчЙћ![]() жадЊЫи
жадЊЫи![]() Тњзу
Тњзу![]() ЃЌОЭГЦ
ЃЌОЭГЦ![]() ЮЊЁАИДЛюМЏЁБЃЌИјГіЯТСаНсТлЃК
ЮЊЁАИДЛюМЏЁБЃЌИјГіЯТСаНсТлЃК
ЂйМЏКЯ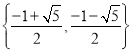 ЪЧЁАИДЛюМЏЁБЃЛ
ЪЧЁАИДЛюМЏЁБЃЛ
ЂкШє![]() ЃЌЧв
ЃЌЧв![]() ЪЧЁАИДЛюМЏЁБЃЌдђ
ЪЧЁАИДЛюМЏЁБЃЌдђ![]() ЃЛ
ЃЛ
ЂлШє![]() ЃЌдђ
ЃЌдђ![]() ВЛПЩФмЪЧЁАИДЛюМЏЁБЃЛ
ВЛПЩФмЪЧЁАИДЛюМЏЁБЃЛ
ЂмШє![]() ЃЌдђЁАИДЛюМЏЁБ
ЃЌдђЁАИДЛюМЏЁБ![]() гаЧвжЛгавЛИіЃЌЧв
гаЧвжЛгавЛИіЃЌЧв![]() .
.
Цфжае§ШЗЕФНсТлЪЧ____________.ЃЈЬюЩЯФуШЯЮЊЫљгае§ШЗЕФНсТлађКХЃЉ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПбЁао4-4ЃКзјБъЯЕгыВЮЪ§ЗНГЬ
дкЦНУцжБНЧзјБъЯЕ![]() жаЃЌЧуаБНЧЮЊ
жаЃЌЧуаБНЧЮЊ![]() ЕФжБЯп
ЕФжБЯп![]() ЕФВЮЪ§ЗНГЬЮЊ
ЕФВЮЪ§ЗНГЬЮЊ![]() ЃЈ
ЃЈ![]() ЮЊВЮЪ§ЃЉ.вдзјБъдЕу
ЮЊВЮЪ§ЃЉ.вдзјБъдЕу![]() ЮЊМЋЕуЃЌ
ЮЊМЋЕуЃЌ![]() жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп
жсе§АыжсЮЊМЋжсНЈСЂМЋзјБъЯЕЃЌЧњЯп![]() ЕФМЋзјБъЗНГЬЮЊ
ЕФМЋзјБъЗНГЬЮЊ![]()
![]() ЃЎ
ЃЎ
ЃЈЂёЃЉЧѓжБЯп![]() ЕФЦеЭЈЗНГЬКЭЧњЯп
ЕФЦеЭЈЗНГЬКЭЧњЯп![]() ЕФжБНЧзјБъЗНГЬЃЛ
ЕФжБНЧзјБъЗНГЬЃЛ
ЃЈЂђЃЉвбжЊЕу![]() ЃЌШєЕу
ЃЌШєЕу![]() ЕФМЋзјБъЮЊ
ЕФМЋзјБъЮЊ![]() ЃЌжБЯп
ЃЌжБЯп![]() ОЙ§Еу
ОЙ§Еу![]() ЧвгыЧњЯп
ЧвгыЧњЯп![]() ЯрНЛгк
ЯрНЛгк![]() СНЕуЃЌЩшЯпЖЮ
СНЕуЃЌЩшЯпЖЮ![]() ЕФжаЕуЮЊ
ЕФжаЕуЮЊ![]() ЃЌЧѓ
ЃЌЧѓ![]() ЕФжЕ.
ЕФжЕ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЕЅЕїЕндіЕФЕШБШЪ§Са![]() Тњзу
Тњзу![]() ,Чв
,Чв![]() ЪЧ
ЪЧ![]() ЕФЕШВюжаЯю.
ЕФЕШВюжаЯю.
(Ђё)ЧѓЪ§Са![]() ЕФЭЈЯюЙЋЪНЃЛ
ЕФЭЈЯюЙЋЪНЃЛ
(Ђђ)Шє![]() ,ЖдШЮвте§Ъ§Ъ§
,ЖдШЮвте§Ъ§Ъ§![]() ЃЌ
ЃЌ ![]() КуГЩСЂЃЌЪдЧѓ
КуГЩСЂЃЌЪдЧѓ![]() ЕФШЁжЕЗЖЮЇ.
ЕФШЁжЕЗЖЮЇ.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПШчЭМ,дкЫФРтзЖ![]() жа,
жа,![]() ,
,![]() ,ЦНУц
,ЦНУц![]() ЕзУц
ЕзУц![]() ,
,![]() ,
,![]() КЭ
КЭ![]() ЗжБ№ЪЧ
ЗжБ№ЪЧ![]() КЭ
КЭ![]() ЕФжаЕу,ЧѓжЄ:
ЕФжаЕу,ЧѓжЄ:
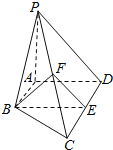
(1)![]() ЕзУц
ЕзУц![]() ;
;
(2)ЦНУц![]() ЦНУц
ЦНУц![]() ;
;
(3)ЦНУц![]() ЦНУц
ЦНУц![]() .
.
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊКЏЪ§fЃЈxЃЉЃНx2+2ax+2ЃЌxЁЪ[Љ5ЃЌ5]ЃЎ
ЃЈ1ЃЉЕБaЃНЉ1ЪБЃЌЧѓКЏЪ§fЃЈxЃЉЕФзюДѓжЕКЭзюаЁжЕЃЛ
ЃЈ2ЃЉМЧКЏЪ§fЃЈxЃЉЕФзюаЁжЕЮЊgЃЈaЃЉЃЌЧѓgЃЈaЃЉЕФБэДяЪНЃЎ
ВщПДД№АИКЭНтЮі>>
ПЦФПЃКИпжаЪ§бЇ РДдДЃК ЬтаЭЃК
ЁОЬтФПЁПвбжЊЭждВ![]() ЕФжааФдкдЕуЃЌРыаФТЪЕШгк
ЕФжааФдкдЕуЃЌРыаФТЪЕШгк![]() ЃЌЫќЕФвЛИіЖЬжсЖЫЕуЧЁКУЪЧХзЮяЯп
ЃЌЫќЕФвЛИіЖЬжсЖЫЕуЧЁКУЪЧХзЮяЯп![]() ЕФНЙЕу.
ЕФНЙЕу.
ЃЈ1ЃЉЧѓЭждВ![]() ЕФЗНГЬЃЛ
ЕФЗНГЬЃЛ
ЃЈ2ЃЉвбжЊ![]() ЁЂ
ЁЂ![]() ЪЧЭждВЩЯЕФСНЕуЃЌ
ЪЧЭждВЩЯЕФСНЕуЃЌ![]() ЪЧЭждВЩЯЮЛгкжБЯп
ЪЧЭждВЩЯЮЛгкжБЯп![]() СНВрЕФЖЏЕу.
СНВрЕФЖЏЕу.
ЂйШєжБЯп![]() ЕФаБТЪЮЊ
ЕФаБТЪЮЊ![]() ЃЌЧѓЫФБпаЮ
ЃЌЧѓЫФБпаЮ![]() УцЛ§ЕФзюДѓжЕЃЛ
УцЛ§ЕФзюДѓжЕЃЛ
ЂкЕБ![]() дЫЖЏЪБЃЌТњзу
дЫЖЏЪБЃЌТњзу![]() ЃЌЪдЮЪжБЯп
ЃЌЪдЮЪжБЯп![]() ЕФаБТЪЪЧЗёЮЊЖЈжЕЃЌЧыЫЕУїРэгЩ.
ЕФаБТЪЪЧЗёЮЊЖЈжЕЃЌЧыЫЕУїРэгЩ.

ВщПДД№АИКЭНтЮі>>
АйЖШжТаХ - СЗЯАВсСаБэ - ЪдЬтСаБэ
КўББЪЁЛЅСЊЭјЮЅЗЈКЭВЛСМаХЯЂОйБЈЦНЬЈ | ЭјЩЯгаКІаХЯЂОйБЈзЈЧј | ЕчаХеЉЦОйБЈзЈЧј | ЩцРњЪЗащЮожївхгаКІаХЯЂОйБЈзЈЧј | ЩцЦѓЧжШЈОйБЈзЈЧј
ЮЅЗЈКЭВЛСМаХЯЂОйБЈЕчЛАЃК027-86699610 ОйБЈгЪЯфЃК58377363@163.com