
| lim | n→∞ |
| 1 |
| 32 |
| 1 |
| 32 |
| 1 |
| 3 |
| 1 |
| 32 |
| 1 |
| 32 |
| 1 |
| 34 |
| 1 |
| 3 |
| 4 |
| 33 |
| 1 |
| 36 |
| 1 |
| 3 |
| 4 |
| 33 |
| 42 |
| 35 |
| 1 |
| 3 |
| 4 |
| 33 |
| 42 |
| 35 |
| 4n-1 |
| 32n-1 |
| 3 |
| 4 |
| n |
 |
| k=1 |
| 4 |
| 9 |
| 8 |
| 5 |
| 3 |
| 5 |
| 4 |
| 9 |
| 8 |
| 5 |
| 3 |
| 5 |
| 4 |
| 9 |
| 1 |
| 32(k+1) |
| 1 |
| 32(k+1) |
| 8 |
| 5 |
| 3 |
| 5 |
| 4 |
| 9 |
| lim |
| n→∞ |
| lim |
| n→∞ |
| 8 |
| 5 |
| 3 |
| 5 |
| 4 |
| 9 |
| 8 |
| 5 |


 高效智能课时作业系列答案
高效智能课时作业系列答案 捷径训练检测卷系列答案
捷径训练检测卷系列答案科目:高中数学 来源: 题型:
 如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).| Tn+1 |
| Tn |
| xn+1 |
| xn |
查看答案和解析>>
科目:高中数学 来源: 题型:
曲线C是平面内到直线l1:x=-1和直线l2:y=1的距离之积等于常数k2![]() 的点的轨迹.给出下列四个结论:
的点的轨迹.给出下列四个结论:
①曲线C过点(-1,1);
②曲线C关于点(-1,1)对称;
③若点P在曲线C上,点A,B分别在直线l1,l2上,则![]() +
+![]() 不小于2k;
不小于2k;
④设P0为曲线C上任意一点,则点P0关于直线x=-1、点(-1,1)及直线y=1对称的点分别为P1、P2、P3,则四边形P0P1P2P3的面积为定值4k2.
其中,所有正确结论的序号是__________________.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
 如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).
如图,过曲线C:y=e-x上一点P0(0,1)做曲线C的切线l0交x轴于Q1(x1,0)点,又过Q1做x轴的垂线交曲线C于P1(x1,y1)点,然后再过P1(x1,y1)做曲线C的切线l1交x轴于Q2(x2,0),又过Q2做x轴的垂线交曲线C于P2(x2,y2),…,以此类推,过点Pn的切线ln与x轴相交于点Qn+1(xn+1,0),再过点Qn+1做x轴的垂线交曲线C于点Pn+1(xn+1,yn+1)(n=1,2,3,…).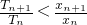 (n∈N+).
(n∈N+).查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| lim |
| n→∞ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com