
【题目】选修4— 4:坐标系与参数方程
设极坐标系与直角坐标系![]() 有相同的长度单位,原点
有相同的长度单位,原点![]() 为极点,
为极点,![]() 轴正半轴为极轴,曲线
轴正半轴为极轴,曲线![]() 的参数方程为
的参数方程为![]() (
(![]() 是参数),直线
是参数),直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(Ⅰ)求曲线![]() 的普通方程和直线
的普通方程和直线![]() 的参数方程;
的参数方程;
(Ⅱ)设点![]() ,若直线
,若直线![]() 与曲线
与曲线![]() 相交于
相交于![]() 两点,且
两点,且![]() ,求
,求![]() 的值﹒
的值﹒
科目:高中数学 来源: 题型:
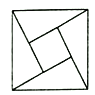
【题目】2002年在北京召开的国际数学家大会的会标是以我国古代数学家的弦图为基础设计的.弦图是由四个全等的直角三角形与一个小正方形拼成的一个大正方形(如图).设其中直角三角形中较小的锐角为![]() ,且
,且![]() ,如果在弦图内随机抛掷1000米黑芝麻(大小差别忽略不计),则落在小正方形内的黑芝麻数大约为( )
,如果在弦图内随机抛掷1000米黑芝麻(大小差别忽略不计),则落在小正方形内的黑芝麻数大约为( )
A. 350B. 300C. 250D. 200
查看答案和解析>>
科目:高中数学 来源: 题型:
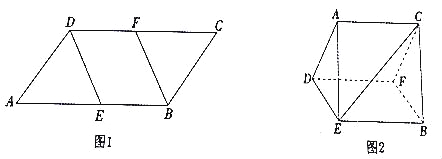
【题目】如图1,在平行四边形![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是
是![]() 的中点,点
的中点,点![]() 是
是![]() 的中点,分别沿
的中点,分别沿![]() .
.![]() 将
将![]() 和
和![]() 折起,使得平面
折起,使得平面![]() 平面
平面![]() (点
(点![]() 在平面
在平面![]() 的同侧),连接
的同侧),连接![]() ,如图2所示.
,如图2所示.
(1)求证:![]() ;
;
(2)当![]() ,且平面
,且平面![]() 平面
平面![]() 时,求三棱锥
时,求三棱锥![]() 的体积.
的体积.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆C:![]() 的右焦点为F(2,0),过点F的直线交椭圆于M、N两点且MN的中点坐标为
的右焦点为F(2,0),过点F的直线交椭圆于M、N两点且MN的中点坐标为![]() .
.
(Ⅰ)求椭圆C的方程;
(Ⅱ)设直线l不经过点P(0,b)且与C相交于A,B两点,若直线PA与直线PB的斜率的和为1,试判断直线 l是否经过定点,若经过定点,请求出该定点;若不经过定点,请给出理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】“水是生命之源”,但是据科学界统计可用淡水资源仅占地球储水总量的![]() ,全世界近
,全世界近![]() 人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准
人口受到水荒的威胁.某市为了鼓励居民节约用水,计划调整居民生活用水收费方案,拟确定一个合理的月用水量标准![]() (吨):一位居民的月用水量不超过
(吨):一位居民的月用水量不超过![]() 的部分按平价收费,超出
的部分按平价收费,超出![]() 的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照
的部分按议价收费.为了了解居民用水情况,通过抽样,获得了某年100位居民每人的月均用水量(单位:吨),将数据按照![]() 分成9组,制成了如图所示的频率分布直方图.
分成9组,制成了如图所示的频率分布直方图.

(1)求直方图中![]() 的值;
的值;
(2)设该市有60万居民,估计全市居民中月均用水量不低于2.5吨的人数,并说明理由;
(3)若该市政府希望使![]() 的居民每月的用水不按议价收费,估计
的居民每月的用水不按议价收费,估计![]() 的值,并说明理由.
的值,并说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥![]() 中,底面
中,底面![]() 是边长为2的菱形,
是边长为2的菱形,![]() ,
,![]() ,平面
,平面![]() 平面
平面![]() ,点
,点![]() 为棱
为棱![]() 的中点.
的中点.

(Ⅰ)在棱![]() 上是否存在一点
上是否存在一点![]() ,使得
,使得![]() 平面
平面![]() ,并说明理由;
,并说明理由;
(Ⅱ)当二面角![]() 的余弦值为
的余弦值为![]() 时,求直线
时,求直线![]() 与平面
与平面![]() 所成的角.
所成的角.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com