
【题目】已知点![]() ,点
,点![]() 为平面上动点,过点
为平面上动点,过点![]() 作直线
作直线![]() 的垂线,垂足为
的垂线,垂足为![]() ,且
,且![]() .
.
(1)求动点![]() 的轨迹方程;
的轨迹方程;
(2)过点![]() 的直线与轨迹
的直线与轨迹![]() 交于
交于![]() 两点,在
两点,在![]() 处分别作轨迹
处分别作轨迹![]() 的切线交于点
的切线交于点![]() ,设直线
,设直线![]() 的斜率分别为
的斜率分别为![]() ,
,![]() ,求证:
,求证:![]() 为定值.
为定值.
【答案】(1)![]() ;(2)
;(2)![]()
【解析】试题分析:(1)设P(x,y),则H(﹣1,y),通过向量的数量积求出动点P的轨迹C的方程.
(2)证明:设点M(x0,y0)(x0≠0)为轨迹C上一点,直线m:y=k0(x﹣x0)+y0为轨迹C的切线,联立在与椭圆方程,利用判别式求出其判别式,求出![]() ,设A(x1,y1),B(x2,y2),AB:y=k(x﹣1),直线与抛物线方程,利用韦达定理求解斜率乘积即可.
,设A(x1,y1),B(x2,y2),AB:y=k(x﹣1),直线与抛物线方程,利用韦达定理求解斜率乘积即可.
试题解析:
(1)设![]() ,则
,则![]() ,有
,有![]() ,
,![]() ,
,![]() ,
,![]() ,从而由题意
,从而由题意![]() ,得动点P的轨迹C的方程y2=4x.
,得动点P的轨迹C的方程y2=4x.
(2)证明:设点![]() (x0≠0)为轨迹C上一点,直线m:y=k0(x-x0)+y0为轨迹C的切线,有
(x0≠0)为轨迹C上一点,直线m:y=k0(x-x0)+y0为轨迹C的切线,有![]() ,消去x得,k0y24y4k0x0+y0=0,其判别式△=16-4k0(-4k0x0+4y0)=0,解得
,消去x得,k0y24y4k0x0+y0=0,其判别式△=16-4k0(-4k0x0+4y0)=0,解得![]() ,有m:
,有m:![]() ,设
,设![]()
得 根据
根据![]()
所以![]() 为定值.
为定值.


科目:高中数学 来源: 题型:
【题目】如图,在正方体![]() 中,过对角线
中,过对角线![]() 的一个平面交
的一个平面交![]() 于点
于点![]() ,交
,交![]() 于
于![]() .
.
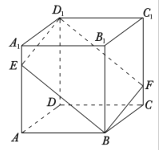
①四边形![]() 一定是平行四边形;
一定是平行四边形;
②四边形![]() 有可能是正方形;
有可能是正方形;
③四边形![]() 在底面
在底面![]() 内的投影一定是正方形;
内的投影一定是正方形;
④四边形![]() 有可能垂直于平面
有可能垂直于平面![]() .
.
以上结论正确的为_______________.(写出所有正确结论的编号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】给出以下四个命题:
①已知命题p:x∈R,tanx=2;命题q:x∈R,x2﹣x+1≥0,则命题p∧q是真命题;
②过点(﹣1,2)且在x轴和y轴上的截距相等的直线方程是x+y﹣1=0;
③函数f(x)=2x+2x﹣3在定义域内有且只有一个零点;
④若直线xsin α+ycos α+l=0和直线 ![]() 垂直,则角
垂直,则角 ![]() .
.
其中正确命题的序号为 . (把你认为正确的命题序号都填上)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图所示,△ABC内接于圆O,D是 ![]() 的中点,∠BAC的平分线分别交BC和圆O于点E,F.
的中点,∠BAC的平分线分别交BC和圆O于点E,F. 
(1)求证:BF是△ABE外接圆的切线;
(2)若AB=3,AC=2,求DB2﹣DA2的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() (
(![]() )离心率等于
)离心率等于![]() ,P(2,3)、Q(2,﹣3)是椭圆上的两点.
,P(2,3)、Q(2,﹣3)是椭圆上的两点.
(1)求椭圆C的方程;
(2)A,B是椭圆上位于直线PQ两侧的动点,若直线AB的斜率为![]() ,求四边形APBQ面积的最大值.
,求四边形APBQ面积的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,在四棱锥中P﹣ABCD,AB=BC=CD=DA,∠BAD=60°,AQ=QD,△PAD是正三角形.
(1)求证:AD⊥PB;
(2)已知点M是线段PC上,MC=λPM,且PA∥平面MQB,求实数λ的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com