
分析 (1)由数列{an}满足${a_1}=\frac{1}{3}$,${a_{n+1}}=\frac{a_n}{{2{a_n}+1}},n∈{N^*}$,可得a2=$\frac{{a}_{1}}{2{a}_{1}+1}$=$\frac{1}{5}$.同理可得:a3,a4.
(2)假设存在正整数p,q使得对任意的n∈N*都有${a_n}=\frac{1}{pn+q}$,则a1=$\frac{1}{p+q}$=$\frac{1}{3}$,a2=$\frac{1}{2p+q}$=$\frac{1}{5}$,解得p=2,q=1.利用数学归纳法证明:${a}_{n}=\frac{1}{2n+1}$即可得出.
解答 解:(1)∵数列{an}满足${a_1}=\frac{1}{3}$,${a_{n+1}}=\frac{a_n}{{2{a_n}+1}},n∈{N^*}$,
∴a2=$\frac{{a}_{1}}{2{a}_{1}+1}$=$\frac{\frac{1}{3}}{2×\frac{1}{3}+1}$=$\frac{1}{5}$.
同理可得:a3=$\frac{1}{7}$,a4=$\frac{1}{9}$.
(2)假设存在正整数p,q使得对任意的n∈N*都有${a_n}=\frac{1}{pn+q}$,
则a1=$\frac{1}{p+q}$=$\frac{1}{3}$,a2=$\frac{1}{2p+q}$=$\frac{1}{5}$,
解得p=2,q=1.
下面利用数学归纳法证明:${a}_{n}=\frac{1}{2n+1}$.
①当n=1时,a1=$\frac{1}{2×1+1}$=$\frac{1}{3}$成立.
②假设n=k∈N*时成立,ak=$\frac{1}{2k+1}$.
则n=k+1时,ak+1=$\frac{{a}_{k}}{2{a}_{k}+1}$=$\frac{\frac{1}{2k+1}}{2×\frac{1}{2k+1}+1}$=$\frac{1}{2(k+1)+1}$,因此n=k+1时成立.
综上可得:对于?n∈N*时,${a}_{n}=\frac{1}{2n+1}$成立.
点评 本题考查了数列递推关系、数学归纳法,考查了推理能力与计算能力,属于中档题.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:选择题
| A. | y=cosx | B. | y=sinx | C. | y=tanx | D. | y=ex |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 84,74 | B. | 88,72 | C. | 73,63 | D. | 88,62 |
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
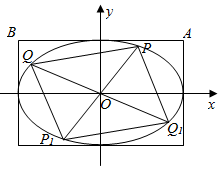 已知椭圆C的中心在原点,对称轴为坐标轴,左焦点为F1(-1,0),离心率为$\frac{1}{2}$.
已知椭圆C的中心在原点,对称轴为坐标轴,左焦点为F1(-1,0),离心率为$\frac{1}{2}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com