已知函数

.
(1)对任意实数

,恒有

,证明

;
(2)若

是方程

的两个实根,

是锐角三角形的两个内角,求证:

。
试题分析:(1)先将函数变形为

,由实数

的任意性可得

,从而可得

。可将问题转化为

时,

恒成立。问题即可得证。(2)分析可知

时,判别式大于0,且可得两根

与系数的关系式。由

是锐角三角形的两个内角可知

,

,即

,

。用正切的两角和差公式可求得

的值。根据以上不等式即可求得

的范围。问题即可得证。
(1) ∵

,
又

, ∴

, 2分
恒有

, 即

时,
恒有

, 即

, 4分
∴

, 又

, 故

. 6分
(2)

,即

,
依题意,得

8分
又A,B为锐角三角形的两内角,∴

, 9分
∴

, 10分
因而

∴

. 12分
练习册系列答案
相关习题
科目:高中数学
来源:不详
题型:解答题
在
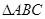
中,角
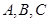
的对边分别为
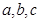
,
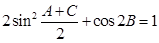
(1)若
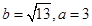
,求
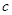
的值;
(2)设
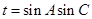
,当
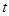
取最大值时求

的值。
查看答案和解析>>
科目:高中数学
来源:不详
题型:单选题
已知
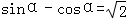
,α∈(0,π),则sin2α=( )
| A.﹣1 | B.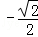 | C.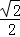 | D.1 |
查看答案和解析>>

 .
. ,恒有
,恒有 ,证明
,证明 ;
; 是方程
是方程 的两个实根,
的两个实根, 是锐角三角形的两个内角,求证:
是锐角三角形的两个内角,求证: 。
。 阅读快车系列答案
阅读快车系列答案