
分析 首先由题意画出图形,利用定积分表示曲边梯形的面积,然后计算定积分.
解答 解:由题意,由曲线y=x2+1与y=3x-1,x=0,x=2所围成的平面图形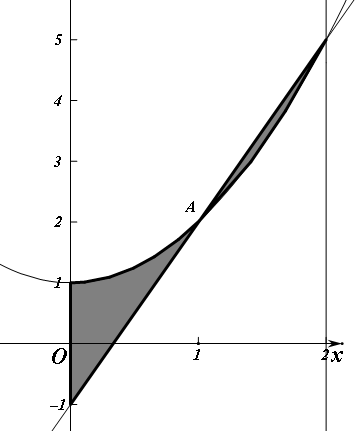 ${S_{阴影}}=\int_1^2{\left\{{3x-1-({x^2}+1)}\right\}}dx$+${∫}_{0}^{1}({x}^{2}+1-3x+1)dx$
${S_{阴影}}=\int_1^2{\left\{{3x-1-({x^2}+1)}\right\}}dx$+${∫}_{0}^{1}({x}^{2}+1-3x+1)dx$
=$\int_1^2{(3x-{x^2}-2)}dx$+${∫}_{1}^{2}$(x2+3x+2)dx
=$(\frac{3}{2}{x}^{2}-\frac{1}{3}{x}^{3}-2x){|}_{1}^{2}$+($\frac{1}{3}{x}^{3}-\frac{3}{2}{x}^{2}+2x$)|${\;}_{0}^{1}$
=$\frac{1}{6}$+$\frac{1}{3}-\frac{3}{2}+2$
=1.
点评 本题考查了利用定积分求曲边梯形的面积,利用数形结合的思想,属于基础题.


科目:高中数学 来源: 题型:解答题
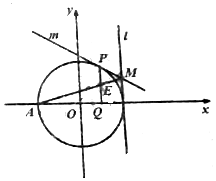 如图,点P是圆O:x2+y2=4上一点,圆O在点P处的切线为m,PQ垂直x轴于点Q(P、Q不重合),线段PQ的重点为E,点A(-2,0),直线l:x=2与直线m交于点M.
如图,点P是圆O:x2+y2=4上一点,圆O在点P处的切线为m,PQ垂直x轴于点Q(P、Q不重合),线段PQ的重点为E,点A(-2,0),直线l:x=2与直线m交于点M.查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | $[{\frac{1}{e^2},1}]$ | B. | $[{\frac{2}{e},1}]$ | C. | $[{\frac{1}{e},1}]$ | D. | [1,e] |
查看答案和解析>>
科目:高中数学 来源: 题型:填空题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com