
【题目】Sn为等差数列{an}的前n项和,且a1=1,S7=28,记bn=[lgan],其中[x]表示不超过x的最大整数,如[0.9]=0,[lg99]=1. (Ⅰ)求b1 , b11 , b101;
(Ⅱ)求数列{bn}的前1000项和.
【答案】解:(Ⅰ)Sn为等差数列{an}的前n项和,且a1=1,S7=28,7a4=28. 可得a4=4,则公差d=1.
an=n,
bn=[lgn],则b1=[lg1]=0,
b11=[lg11]=1,
b101=[lg101]=2.
(Ⅱ)由(Ⅰ)可知:b1=b2=b3=…=b9=0,b10=b11=b12=…=b99=1.
b100=b101=b102=b103=…=b999=2,b10 , 00=3.
数列{bn}的前1000项和为:9×0+90×1+900×2+3=1893
【解析】(Ⅰ)利用已知条件求出等差数列的公差,求出通项公式,然后求解b1 , b11 , b101;(Ⅱ)找出数列的规律,然后求数列{bn}的前1000项和.
【考点精析】本题主要考查了数列的前n项和和等差数列的性质的相关知识点,需要掌握数列{an}的前n项和sn与通项an的关系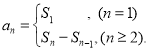 ;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列才能正确解答此题.
;在等差数列{an}中,从第2项起,每一项是它相邻二项的等差中项;相隔等距离的项组成的数列是等差数列才能正确解答此题.


 中考解读考点精练系列答案
中考解读考点精练系列答案科目:高中数学 来源: 题型:
【题目】已知梯形CEPD如图(1)所示,其中PD=8,CE=6,A为线段PD的中点,四边形ABCD为正方形,现沿AB进行折叠,使得平面PABE⊥平面ABCD,得到如图(2)所示的几何体.已知当点F满足 ![]() =
= ![]() (0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( )
(0<λ<1)时,平面DEF⊥平面PCE,则λ的值为( ) 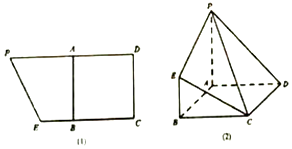
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知△ABC中,内角A,B,C所对的边分别为a,b,c,且满足asinA﹣csinC=(a﹣b)sinB.
(1)求角C的大小;
(2)若边长 ![]() ,求△ABC的周长最大值.
,求△ABC的周长最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】《莱因德纸草书》(Rhind Papyrus)是世界上最古老的数学著作之一.书中有一道这样的题目:把100个面包分给5个人,使每个人所得成等差数列,且使较大的三份之和的 ![]() 是较小的两份之和,问最小一份为( )
是较小的两份之和,问最小一份为( )
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】将函数y=sinx的图象向右平移三个单位长度得到图象C,再将图象C上的所有点的横坐标变为原来的![]() 倍(纵坐标不变)得到图象C1 , 则C1的函数解析式为
倍(纵坐标不变)得到图象C1 , 则C1的函数解析式为
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,∠C= ![]() ,AC=BC,M、N分别是BC、AB的中点,将△BMN沿直线MN折起,使二面角B′﹣MN﹣B的大小为
,AC=BC,M、N分别是BC、AB的中点,将△BMN沿直线MN折起,使二面角B′﹣MN﹣B的大小为 ![]() ,则B'N与平面ABC所成角的正切值是( )
,则B'N与平面ABC所成角的正切值是( ) 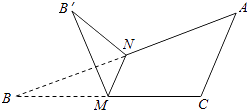
A.![]()
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】在棱长都相等的四面体P-ABC中,D、E、F分别是AB、BC、CA的中点,则下面四个结论中不成立的是 ( )
A.BC∥平面PDF
B.DF⊥平面PAE
C.平面PDF⊥平面ABC
D.平面PAE⊥平面ABC
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com