练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情
    19．执行如图所示的程序框图，输出的y值为（　　）
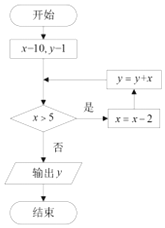
    A．15B．17C．19D．21

    分析 根据所给数值先执行一次运算，然后判定是否满足判断框中的条件，不满足执行循环语句，满足条件就退出循环，从而到结论

    解答 解：x=10，y=1，x＞5，x=8，y=9，
    x＞5，x=6，y=15，
    x＞5，x=4，y=21，
    输出y=21，
    故选：D．

    点评 本题主要考查了循环结构，解答的关键是明确判断框内的条件，不满足条件进入循环体，满足条件，结束算法．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：选择题

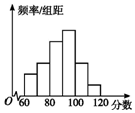    9．为了了解高三学生的数学成绩，抽取了某班60名学生，将所得数据整理后，画出其频率分布直方图，如图．已知从左到右各长方形高的比为2：3：5：6：3：1，则该班学生数学成绩在[80，100）之间的学生人数是（　　）
    A．32B．27C．24D．33

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    10．已知点A是抛物线x2=4y的对称轴与准线的交点，点F为抛物线的焦点，P在抛物线上且满足|PA|=m|PF|，当m取最大值时|PA|的值为（　　）
    A．1B．$\sqrt{5}$C．$\sqrt{6}$D．2$\sqrt{2}$

    查看答案和解析>>

    科目：高中数学 来源： 题型：解答题

    7．曲线C1的参数方程为$\left\{\begin{array}{l}{x=2+2cosα}\\{y=2sinα}\end{array}\right.$（α为参数）在以原点O为极点，x轴的非负半轴为极轴的极坐标系中，曲线C2的极坐标方程为ρcos2θ=sinθ．
    （1）求曲线C1的极坐标方程和曲线C2的直角坐标方程；
    （2）过原点且倾斜角为α（$\frac{π}{6}$＜α≤$\frac{π}{4}$）的射线l与曲线C1，C2分别相交于A，B两点（A，B异于原点），求|OA|•|OB|的取值范围．

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    14．若变量x，y满足条件$\left\{\begin{array}{l}x-y-1≤0\\ x+y-6≤0\\ x-3≥0\end{array}\right.$，则xy的取值范围是（　　）
    A．[0，5]B．$[{5，\frac{35}{4}}]$C．$[{0，\frac{35}{4}}]$D．[6，9]

    查看答案和解析>>

    科目：高中数学 来源： 题型：选择题

    4．在同一平面直角坐标系中经过伸缩变换$\left\{\begin{array}{l}x'=5x\\ y'=3y\end{array}\right.$后，曲线C变为曲线2x′2+8y′2=1，则曲线C的方程为（　　）
    A．25x2+36y2=1B．50x2+72y2=1C．10x2+24y2=1D．$\frac{{2{x^2}}}{25}+\frac{{8{y^2}}}{9}=1$

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    11．已知数列{an}中，an=n，前n项和为Sn，则$\frac{1}{{S}_{1}}$+$\frac{1}{{S}_{2}}$+…+$\frac{1}{{S}_{100}}$=$\frac{200}{101}$．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    8．若α是第四象限，则180°-α是第三象限角．

    查看答案和解析>>

    科目：高中数学 来源： 题型：填空题

    9．在以O为极点的极坐标系中，曲线ρ=2cosθ和直线ρcosθ=a相交于A，B两点．若△AOB是等边三角形，则a的值为$\frac{3}{2}$．

    查看答案和解析>>

    同步练习册答案