
(12分) 若二次函数f(x)=ax2+bx+c(a≠0)的图象关于y轴对称,
且f(-2)>f(3),设m>-n>0.
(1) 试证明函数f(x)在(0,+∞)上是减函数;
(2) 试比较f(m)和f(n)的大小,并说明理由.
科目:高中数学 来源: 题型:解答题
已知函数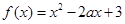
(1)若函数在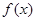 的单调递减区间(—∞,2],求函数
的单调递减区间(—∞,2],求函数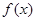 在区间[3,5]上的最大值.
在区间[3,5]上的最大值.
(2)若函数在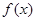 在单区间(—∞,2]上是单调递减,求函数
在单区间(—∞,2]上是单调递减,求函数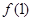 的最大值.
的最大值.
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
某同学利用暑假时间到一家商场勤工俭学,该商场向他提供了三种付款方式:第一种,每天支付38圆;第二种,第一天付4元,第二天付8元,第三天付12元,以此类推:第三种,第一天付0.4元,以后每天比前一天翻一番(即增加一倍),
你会选择哪种方式领取报酬呢?
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
已知函数 定义域为
定义域为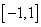 ,若对于任意的
,若对于任意的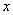 ,
,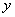
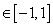 ,都有
,都有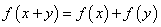 ,且
,且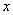 >0时,有
>0时,有 >0.
>0.
⑴证明:  为奇函数;
为奇函数;
⑵证明:  在
在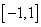 上为单调递增函数;
上为单调递增函数;
⑶设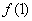 =1,若
=1,若 <
<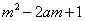 ,对所有
,对所有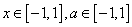 恒成立,求实数
恒成立,求实数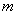 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com