
甲乙两人进行乒乓球比赛,约定每局胜者得1分,负者得0分,比赛进行到有一人比对方多2分或打满6局时停止.设甲在每局中获胜的概率为 ,乙在每局中获胜的概率为
,乙在每局中获胜的概率为 ,且各局胜负相互独立,比赛停止时一共已打
,且各局胜负相互独立,比赛停止时一共已打 局:
局:
(1)列出随机变量 的分布列;
的分布列;
(2)求 的期望值E
的期望值E .
.
(1)
(2)ξ 2 4 6 P 



解析试题分析:(1)先列出随机变量
科目:高中数学
来源:
题型:解答题
有甲、乙两个盒子,甲盒子中有8张卡片,其中2张写有数字0,3张写有数字1,3张写有数字2;乙盒子中有8张卡片,其中3张写有数字0,2张写有数字1,3张写有数字2.
科目:高中数学
来源:
题型:解答题
一个袋子中装有7个小球,其中红球4个,编号分别为1,2,3,4,黄球3个,编号分别为2,4,6,从袋子中任取4个小球(假设取到任一小球的可能性相等).
科目:高中数学
来源:
题型:解答题
一个口袋装有n个红球(n≥5且n∈N)和5个白球,一次摸奖从中摸2个球(每次摸奖后放回),2个球颜色不同则为中奖.
科目:高中数学
来源:
题型:解答题
某市质监部门对市场上奶粉进行质量抽检,现将9个进口品牌奶粉的样品编号为1,2,3,4, ,9;6个国产品牌奶粉的样品编号为10,11,12,15,按进口品牌及国产品牌分层进行分层抽样,从其中抽取5个样品进行首轮检验,用
科目:高中数学
来源:
题型:解答题
已知甲盒内有大小相同的1个红球和3个黑球,乙盒内有大小相同的2个红球和4个黑球,现从甲、乙两个盒内各任取2个球.
科目:高中数学
来源:
题型:解答题
已知复数z=x+yi(x,y∈R)在复平面上对应的点为M.
科目:高中数学
来源:
题型:解答题
一投掷飞碟的游戏中,飞碟投入红袋记2分,投入蓝袋记1分,未投入袋记0分.经过多次试验,某人投掷100个飞碟有50个入红袋,25个入蓝袋,其余不能入袋.
科目:高中数学
来源:
题型:解答题
某活动将在辽宁沈阳举行,组委会在沈阳某大学招募了12名男志愿者和18名女志愿者,将这30名志愿者的身高编成如图所示的茎叶图(单位:cm),身高在175 cm以上(包括175 cm)定义为“高个子”,身高在175 cm以下(不包括175 cm)定义为“非高个子”.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区 所有可能值,为2,4,6.再分别讨论三种情况下,两者输赢情况,需全面考虑,不能遗漏,如
所有可能值,为2,4,6.再分别讨论三种情况下,两者输赢情况,需全面考虑,不能遗漏,如 时,甲可以全赢,也可全输,不能一赢一输;
时,甲可以全赢,也可全输,不能一赢一输; 时,前两局必是甲一赢一输;而后两局必是某人全赢;
时,前两局必是甲一赢一输;而后两局必是某人全赢; 时,可利用概率和为
时,可利用概率和为 ,求其“补集”即可;也可直接计算,此时需要注意前四局分布情况是:前两局必是甲一赢一输;接下来的两局也必是甲一赢一输,但最后的两局却没有限制;(2)利用期望值计算公式Eξ=2×
,求其“补集”即可;也可直接计算,此时需要注意前四局分布情况是:前两局必是甲一赢一输;接下来的两局也必是甲一赢一输,但最后的两局却没有限制;(2)利用期望值计算公式Eξ=2× +4×
+4× +6×
+6× =
=
试题解析:解法1:
(1)依题意知,ξ的所有可能值为2,4,6.
设每两局比赛为一轮,则该轮结束时比赛停止的概率为( )2+(
)2+( )2=
)2= . 4分
. 4分
若该轮结束时比赛还将继续,则甲、乙在该轮中必是各得一分,此时,该轮比赛结果对下轮比赛是否停止没有影响.从在则有 , 7分
, 7分
∴ξ的分布列为
9分ξ 2 4 6 P 


(2)Eξ=2× +4×
+4× +6×
+6× =
= . 12分
. 12分
解法2:(1)依题意知,ξ的所有可能值为2,4,6.
令Ak表示甲在第k局比赛中获胜,则 k表示乙在第k局比赛中获胜.
k表示乙在第k局比赛中获胜.
由独立性与互斥性得 =P(A1A2)+P(
=P(A1A2)+P(
 )=
)= , 2分
, 2分 =P(
=P( )+P(
)+P( )+P(
)+P( )+P(
)+P( )
)
=2[( )3(
)3( )+(
)+( )3(
)3( )]=
)]= , 4分
, 4分 =P(
=P( )+P(
)+P( )+P(
)+P( )+P(
)+P( )
)
=4( )2(
)2( )2=
)2= , 7分
, 7分
∴ξ的分布列为

解决问题专项训练系列答案
应用题夺冠系列答案
小学生生活系列答案
小学毕业总复习系列答案
优翼专项小学升学总复习系统强化训练系列答案
小学升初中夺冠密卷系列答案
小学升初中核心试卷系列答案
小学升初中进重点校必练密题系列答案
期末测试卷系列答案
小学培优总复习系列答案
(1)如果从甲盒子中取2张卡片,从乙盒中取1张卡片,那么取出的3张卡片都写有1的概率是多少?
(2)如果从甲、乙两个盒子中各取1张卡片,设取出的两张卡片数字之和为X,求X的概率分布.
(1)求取出的小球中有相同编号的概率;
(2)记取出的小球的最大编号为 ,求随机变量
,求随机变量 的分布列和数学期望.
的分布列和数学期望.
(1)试用n表示一次摸奖中奖的概率.
(2)若n=5,求3次摸奖的中奖次数ξ=1的概率及数学期望.
(3)记3次摸奖恰有1次中奖的概率为P,当n取多少时,P最大? 表示编号为
表示编号为
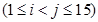 的样品首轮同时被抽到的概率.
的样品首轮同时被抽到的概率.
(1)求 的值;
的值;
(2)求所有的
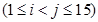 的和.
的和.
(1)求取出的4个球均为黑球的概率.
(2)求取出的4个球中恰有1个红球的概率.
(1)设集合P={-4,-3,-2,0},Q={0,1,2},从集合P中随机取一个数作为x,从集合Q中随机取一个数作为y,求复数z为纯虚数的概率.
(2)设x∈[0,3],y∈[0,4],求点M落在不等式组: 所表示的平面区域内的概率.
所表示的平面区域内的概率.
(1)求该人在4次投掷中恰有三次投入红袋的概率;
(2)求该人两次投掷后得分ξ的数学期望Eξ.
(1)如果用分层抽样的方法从“高个子”和“非高个子”中共抽取5人,再从这5人中选2人,求至少有一人是“高个子”的概率;
(2)若从身高180 cm以上(包括180 cm)的志愿者中选出男、女各一人,求这2人身高相差5 cm以上的概率.
版权声明:本站所有文章,图片来源于网络,著作权及版权归原作者所有,转载无意侵犯版权,如有侵权,请作者速来函告知,我们将尽快处理,联系qq:3310059649。
ICP备案序号: 沪ICP备07509807号-10 鄂公网安备42018502000812号