
已知定义在R上的函数f(x)满足f(x+1)=-f(x)。当x [0,1]时,f(x)=
[0,1]时,f(x)=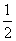 -x,若g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,则实数m的取值范围是
-x,若g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点,则实数m的取值范围是
A.(-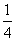 ,
, ) B.(-
) B.(-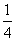 ,
, ] C.
] C.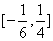 D.
D.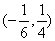
B
【解析】
试题分析:根据题意,可求出f(x)区间(-1,2]上的分段函数的表达式,然后在同一坐标系内作出y=f(x)和y=m(x+1)的图象,观察直线y=m(x+1)的斜率m变化,可得直线y=m(x+1)位于图中AB、AC之间(包括AC)活动时,两个图象有三个公共点,由此求出直线AB、AC的斜率并与实数m加以比较,即可得到本题的答案.解:设得x+1∈[0,1],此时f(x+1)= -(x+1)=-x-
-(x+1)=-x- ,
,
∵函数f(x)满足f(x+1)=-f(x)

∴当-1≤x≤0时,f(x)=x+ .又∵f(x+2)=-f(x+1)═-[f(-x)]=f(x)∴f(x)是以2为周期的函数,可得当1≤x≤2时,f(x)=f(x-2)=x-
.又∵f(x+2)=-f(x+1)═-[f(-x)]=f(x)∴f(x)是以2为周期的函数,可得当1≤x≤2时,f(x)=f(x-2)=x- 综上所述,得f(x)区间(-1,2]上的表达式为f(x)=
综上所述,得f(x)区间(-1,2]上的表达式为f(x)=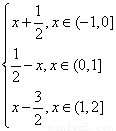 ,
,
为了研究g(x)=f(x)-m(x+1)在区间(-1,2]上的零点,将其形为,f(x)=m(x+1),在同一坐标系内作出y=f(x)和y=m(x+1)的图象,如右图所示,y=f(x)图象是三条线段构成的折线,y=m(x+1)的图象是直线,因为直线y=m(x+1)经过定点A(-1,0),所以由图象可得当直线y=m(x+1),位于图中AB、AC之间(包括AC)活动时,两个图象有三个公共点,相应地,g(x)=f(x)-m(x+1)在区间(-1,2]也有3个零点,∵B(1,-0.5),C(2,0.5),,∴kAB= 而直线y=m(x+1)的斜率为m,它在AB、AC之间(包括AC)活动时,m(
而直线y=m(x+1)的斜率为m,它在AB、AC之间(包括AC)活动时,m( ,
,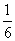 ].因此,使得g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点的m取值范围为m(
].因此,使得g(x)=f(x)-m(x+1)在区间(-1,2]有3个零点的m取值范围为m( ,
,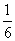 ],故选B
],故选B
考点:分段函数图象
点评:本题给出分段函数图象与直线有三个公共点,求直线斜率m的取值范围,着重考查了基本初等函数的图象与性质、直线的斜率及其变化等知识,属于中档题


 金状元绩优好卷系列答案
金状元绩优好卷系列答案科目:高中数学 来源: 题型:
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
|
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、-2 | B、2 | C、4 | D、-4 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| A、0 | B、2013 | C、3 | D、-2013 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com