Question

2．给出下列命题：
①函数$f（x）=4cos（2x+\frac{π}{3}）$的一个对称中心为$（-\frac{5}{12}π，0）$
②已知：f（x）=min{sinx，cosx}，则f（x）的值域为$[-1，\frac{{\sqrt{2}}}{2}]$
③若α，β均为第一象限角，且α＞β，则sinα＞sinβ
④若${（\frac{1}{2}）^a}={（\frac{1}{3}）^b}$，则a＞b＞0
⑤定义域为R的函数y=f（x）满足f（-x）+f（x+2）=2，则其图象关于点（1，1）对称
其中正确命题的序号是①②⑤（写出所有正确命题的序号）

Answer 1

分析 ①令2x+$\frac{π}{3}$=$kπ+\frac{π}{2}$，解得x=$\frac{kπ}{2}$+$\frac{π}{12}$，令k=-1，即可判断出正误；
②f（x）=min{sinx，cosx}，画出一个周期的图象，即可判断出正误；
③不正确，举反例：$α=2π+\frac{π}{6}$，$β=\frac{π}{3}$；
④若${（\frac{1}{2}）^a}={（\frac{1}{3}）^b}$，如图所示：即可判断出正误；
⑤定义域为R的函数y=f（x）：则点（-x，f（-x））关于点（1，1）对称的点为（2+x，f（2+x）），由于满足f（-x）+f（x+2）=2，即可判断出函数f（x）的图象的对称性．

解答 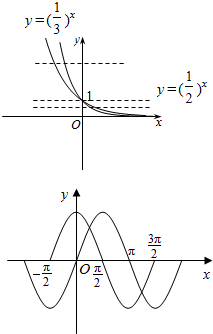解：①令2x+$\frac{π}{3}$=$kπ+\frac{π}{2}$，解得x=$\frac{kπ}{2}$+$\frac{π}{12}$，令k=-1，可得x=$-\frac{5π}{12}$，因此函数$f（x）=4cos（2x+\frac{π}{3}）$的一个对称中心为$（-\frac{5}{12}π，0）$，正确；
②f（x）=min{sinx，cosx}，画出一个周期的图象，则f（x）的值域为$[-1，\frac{{\sqrt{2}}}{2}]$，正确；
③若α，β均为第一象限角，且α＞β，则sinα＞sinβ，不正确，举反例：$α=2π+\frac{π}{6}$，$β=\frac{π}{3}$；
④若${（\frac{1}{2}）^a}={（\frac{1}{3}）^b}$，如图所示：
则a＞b＞0，或a=b=0，或 a＜b＜0，因此不正确；
⑤定义域为R的函数y=f（x）：则点（-x，f（-x））关于点（1，1）对称的点为
（2+x，f（2+x）），由于满足f（-x）+f（x+2）=2，因此其图象关于点（1，1）对称，正确．
其中正确命题的序号是①②⑤．
故答案为：①②⑤．

点评 本题考查了三角函数的图象与性质、指数函数的图象与单调性、函数对称性、简易逻辑的判定方法，考查了数形结合思想方法、推理能力与计算能力，属于中档题．