【题目】东方商店欲购进某种食品（保质期一天），此商店每两天购进该食品一次（购进时，该食品为刚生产的）.根据市场调查，该食品每份进价
元，售价
元，如果一天内无法售出，则食品过期作废，现统计该产品
天的销售量如下表：
（1）根据该产品天的销售量统计表，求平均每天销售多少份？
（2）视样本频率为概率，以一天内该产品所获得的利润的平均值为决策依据，东方商店一次性购进
或
份，哪一种得到的利润更大？
名校课堂系列答案科目：高中数学 来源： 题型：
【题目】己知抛物线C：x2=4y的焦点为F，直线l与抛物线C交于A，B两点，延长AF交抛物线C于点D，若AB的中点纵坐标为|AB|-1，则当∠AFB最大时，|AD|=（ ）
A. 4B. 8C. 16D. 
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】在梯形
中，
，
为
的中点，线段
与
交于
点（如图1）.将
沿折起到
的位置，使得二面角
为直二面角（如图2）.
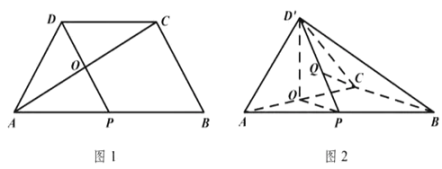
（1）求证：
平面
；
（2）线段
上是否存在点
，使得
与平面
所成角的正弦值为
？若存在，求出
的值；若不存在，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】我市为增强市民的环境保护意识，面向全市征召义务宣传志愿者.现从符合条件的志愿者中随机抽取100名按年龄（单位：岁）分组：第1组
，第2组
，第3组
，第4组
，第5组
，得到的频率分布直方图如图所示.
（1）若从第3，4，5组中用分层抽样的方法抽取6名志愿者参加广场的宣传活动，应从第3，4，5组各抽取多少名志愿者？
（2）请根据频率分布直方图，估计这100名志愿者样本的平均数；
（3）在（1）的条件下，该市决定在这6名志愿者中随机抽取2名志愿者介绍宣传经验，求第4组至少有一名志愿者被抽中的概率.（参考数据：
）
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】已知椭圆
（
）的左右焦点分别为
，
，已知其离心率为
，且过点
.
（1）求椭圆的标准方程.
（2）设
，
是椭圆上位于
轴上方的两点，且直线
与直线
平行，
与
交于点
，探究
是否为定值？如果为定值，请求出该定值；如果不为定值，请说明理由.
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】某城市收集并整理了该市2017年1月份至10月份每月份最低气温与最高气温（单位：
）的数据，绘制了折线图（如图）.已知该市每月的最低气温与当月的最高气温两变量具有较好的线性关系，则根据该折线图，下列结论错误的是（）
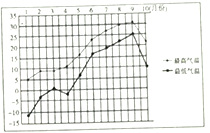
A. 最低气温低于
的月份有
个
B. 
月份的最高气温不低于
月份的最高气温
C. 月温差（最高气温减最低气温）的最大值出现在
月份
D. 每月份最低气温与当月的最高气温两变量为正相关
查看答案和解析>>
科目：高中数学 来源： 题型：
【题目】新个税法于2019年1月1日进行实施.为了调查国企员工对新个税法的满意程度，研究人员在
地各个国企中随机抽取了1000名员工进行调查，并将满意程度以分数的形式统计成如下的频率分布直方图，其中
.
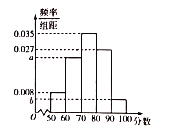
（1）求
的值并估计被调查的员工的满意程度的中位数；（计算结果保留两位小数）
（2）若按照分层抽样从
，
中随机抽取8人，再从这8人中随机抽取2人，求至少有1人的分数在的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com
