分析:解法一:(Ⅰ)(i)先证明FD∥平面AGH,CD∥平面AGH,再利用面面平行的判定定理,即可证明平面CDF∥平面AGH;
(ii)确定∠CED或其补角即为异面直线AB与CE所成的角,再用余弦定理,即可求异面直线AB与CE所成角的正切值;
(Ⅱ)确定∠CDF即为二面角C-DE-F的平面角,再用余弦定理求二面角C-DE-F的余弦值.
解法二:(Ⅰ)(i)同解法一;
(ii)建立空间直角坐标系,确定
,的坐标,利用向量的夹角公式,即可求异面直线AB与CE所成角的正切值;
(Ⅱ)确定平面CDE、平面DEF的法向量,利用向量的夹角公式,即可求二面角C-DE-F的余弦值.
解答: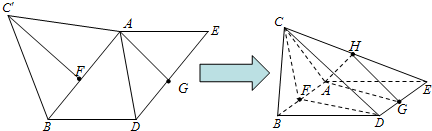
解法一:(Ⅰ) (i)证明:连FD.因为ABDE为平行四边形,F、G分别为AB、DE中点,
所以FDGA为平行四边形,所以FD∥AG.----------------------(1分)
又H、G分别为CE、DE的中点,所以HG∥CD.------------------(2分)
因为FD、CD?平面AGH,AG、HG?平面AGH,所以FD∥平面AGH,CD∥平面AGH,
而FD、CD?平面CDF,所以平面CDF∥平面AGH.---------------(4分)
(ii)解:因为DE∥AB,所以∠CED或其补角即为异面直线AB与CE所成的角.-----------(5分)
因为ABC为正三角形,BD=AD,F为AB中点,所以AB⊥CF,AB⊥DF,从而AB⊥平面CFD,
而DE∥AB,所以DE⊥平面CFD,
因为CD?平面CFD,所以DE⊥CD.--------------------------(7分)
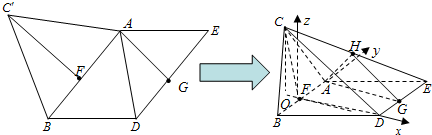
由条件易得
CF=4 , DF==3,
又∠CFD为二面角C-AB-D的平面角,所以∠CFD=120°,
所以
CD==,
所以
tan∠CED==.---------------------(9分)
(Ⅱ) 解:由(Ⅰ)的(ii)知DE⊥平面CFD,即CD⊥DE,FD⊥DE,所以∠CDF即为二面角C-DE-F的平面角.---(12分)
所以
cos∠CDF===.---------------(14分)
解法二:(Ⅰ) (i)同解法一;
(ii) 因为ABC为正三角形,BD=AD,F为AB中点,所以AB⊥CF,AB⊥DF,从而∠CFD为二面角C-AB-D的平面角且AB⊥平面CFD,而AB?平面ABDE,所以平面CFD⊥平面ABDE.
作CO⊥平面ABDE于O,则O在直线DF上,又由二面角C-AB-D的平面角为∠CFD=120°,故O在线段DF的延长线上.
由
CF=4得
FO=2 , CO=6.--------(6分)
以F为原点,FA、FD、FZ为x、y、z轴建立空间直角坐标系,如图,则由上述及已知条件得各点坐标为A(0,4,0),B(0,-4,0),
D(3 , 0 , 0),
E(3 , 8 , 0),
C(-2 , 0 , 6),
所以
=(0 , -8 , 0),
=(5 , 8 , -6).----------------(8分)
所以异面直线AB与CE所成角的余弦值为
|cos( , )|===,
从而其正切值为
=.------------------------------(10分)
(Ⅱ)由(Ⅰ)的(ii)知
=(5 , 0 , -6) , =(0 , 8 , 0),
设平面CDE的法向量为
=(x,y,z),则由
⊥
,
⊥
得
令
z=5,得
=
(6 , 0 , 5).-----------(12分)
又平面DEF的一个法向量为
=(0,0,1),而二面角C-DE-F为锐二面角,
所以二面角C-DE-F的余弦为
|cos<, >|==.-------------(14分)

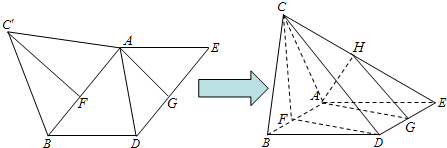
 解法一:(Ⅰ) (i)证明:连FD.因为ABDE为平行四边形,F、G分别为AB、DE中点,
解法一:(Ⅰ) (i)证明:连FD.因为ABDE为平行四边形,F、G分别为AB、DE中点,

