
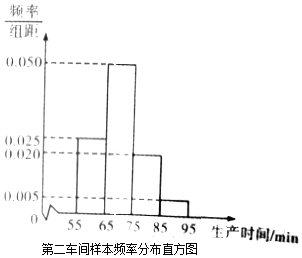
【题目】某工厂有两个车间生产同一种产品,第一车间有工人200人,第二车间有工人400人,为比较两个车间工人的生产效率,采用分层抽样的方法抽取工人,并对他们中每位工人生产完成一件产品的时间(单位:min)分别进行统计,得到下列统计图表(按照[55,65),[65,75),[75,85),[85,95]分组).
分组 | 频数 |
[55,65) | 2 |
[65,75) | 4 |
[75,85) | 10 |
[85,95] | 4 |
合计 | 20 |
第一车间样本频数分布表
(Ⅰ)分别估计两个车间工人中,生产一件产品时间小于75min的人数;
(Ⅱ)分别估计两车间工人生产时间的平均值,并推测哪个车间工人的生产效率更高?(同一组中的数据以这组数据所在区间中点的值作代表)
(Ⅲ)从第一车间被统计的生产时间小于75min的工人中,随机抽取3人,记抽取的生产时间小于65min的工人人数为随机变量X,求X的分布列及数学期望.
【答案】(I)60,300;(II)第二车间工人生产效率更高.(III)见解析.
【解析】
(I)估计第一车间生产时间小于75min的工人人数为![]() (人).估计第二车间生产时间小于75min的工人人数为
(人).估计第二车间生产时间小于75min的工人人数为![]() (人);(II)分别计算两车间工人生产时间的平均值,再推测哪个车间工人的生产效率更高;(III)由题得X可取值为0,1,2,再分别求出概率,列出分布列,求出数学期望.
(人);(II)分别计算两车间工人生产时间的平均值,再推测哪个车间工人的生产效率更高;(III)由题得X可取值为0,1,2,再分别求出概率,列出分布列,求出数学期望.
(I)估计第一车间生产时间小于75min的工人人数为![]() (人).
(人).
估计第二车间生产时间小于75min的工人人数为![]() (人).
(人).
(II)第一车间生产时间平均值约为![]() (min).
(min).
第二车间生产时间平均值约为![]()
(min).
∴第二车间工人生产效率更高.
(III)由题意得,第一车间被统计的生产时间小于75min的工人有6人,其中生产时间小于65min的有2人,从中抽取3人,随机变量X服从超几何分布,
X可取值为0,1,2,
![]() ,
,
![]() ,
,
![]() .
.
X的分布列为:
X | 0 | 1 | 2 |
P |
|
|
|
所以数学期望![]() .
.


科目:高中数学 来源: 题型:
【题目】给出下列四个说法,其中正确的是( )
A.命题“若![]() ,则
,则![]() ”的否命题是“若
”的否命题是“若![]() ,则
,则![]() ”
”
B.“![]() ”是“双曲线
”是“双曲线![]() 的离心率大于
的离心率大于![]() ”的充要条件
”的充要条件
C.命题“![]() ,
,![]() ”的否定是“
”的否定是“![]() ,
,![]() ”
”
D.命题“在![]() 中,若
中,若![]() ,则
,则![]() 是锐角三角形”的逆否命题是假命题
是锐角三角形”的逆否命题是假命题
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】(1)已知数列![]() 为等差数列,其前n项和为
为等差数列,其前n项和为![]() .若
.若![]() ,试分别比较
,试分别比较![]() 与
与![]() 、
、![]() 与
与![]() 的大小关系.
的大小关系.
(2)已知数列![]() 为等差数列,
为等差数列,![]() 的前n项和为
的前n项和为![]() .证明:若存在正整数k,使
.证明:若存在正整数k,使![]() ,则
,则![]() .
.
(3)在等比数列![]() 中,设
中,设![]() 的前n项乘积
的前n项乘积![]() ,类比(2)的结论,写出一个与
,类比(2)的结论,写出一个与![]() 有关的类似的真命题,并证明.
有关的类似的真命题,并证明.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知直线l经过抛物线y2=6x的焦点F,且与抛物线相交于A,B两点.
(1)若直线l的倾斜角为60°,求|AB|的值;
(2)若|AB|=9,求线段AB的中点M到准线的距离.
查看答案和解析>>
科目:高中数学 来源: 题型:
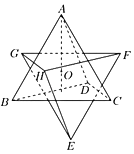
【题目】正四面体ABCD的体积为1,O为其中心,正四面体EFGH与正四面体ABCD关于点O对称,则这两个正四面体的公共部分的体积为( )
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() .
.
(1)若曲线![]() 在点
在点![]() 处的切线与直线
处的切线与直线![]() 垂直,求函数
垂直,求函数![]() 的单调区间;
的单调区间;
(2)若对于任意![]() 都有
都有![]() 成立,试求
成立,试求![]() 的取值范围;
的取值范围;
(3)记![]() .当
.当![]() 时,函数
时,函数![]() 在区间
在区间![]() 上有两个零点,求实数
上有两个零点,求实数![]() 的取值范围。
的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com