
【题目】在下列向量组中,可以把向量![]() =(3,2)表示出来的是( )
=(3,2)表示出来的是( )
A. ![]() =(0,0),
=(0,0),![]() =(1,2)B.
=(1,2)B. ![]() =(-1,2),
=(-1,2),![]() =(5,-2)
=(5,-2)
C. ![]() =(3,5),
=(3,5),![]() =(6,10)D.
=(6,10)D. ![]() =(2,-3),
=(2,-3),![]() =(-2,3)
=(-2,3)
 字词句篇与同步作文达标系列答案
字词句篇与同步作文达标系列答案 走进文言文系列答案
走进文言文系列答案科目:高中数学 来源: 题型:
【题目】下列四个命题:
①圆![]() 与直线
与直线![]() 相交,所得弦长为
相交,所得弦长为![]() ;
;
②直线![]() 与圆
与圆![]() 恒有公共点;
恒有公共点;
③若棱长为![]() 的正方体的顶点都在同一球面上,则该球的表面积为
的正方体的顶点都在同一球面上,则该球的表面积为![]() ;
;
④若棱长为![]() 的正四面体的顶点都在同一球面上,则该球的体积为
的正四面体的顶点都在同一球面上,则该球的体积为![]() .
.
其中,正确命题的序号为__________.(写出所有正确命题的序号)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】定义域为R的函数f(x)满足:对于任意的实数x,y都有f(x+y)=f(x)+f(y)成立,且当x<0时,f(x)>0恒成立,且nf(x)=f(nx).(n是一个给定的正整数).
(1)判断函数f(x)的奇偶性,并证明你的结论;
(2)证明f(x)为减函数;若函数f(x)在[-2,5]上总有f(x)≤10成立,试确定f(1)应满足的条件;
(3)当a<0时,解关于x的不等式![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了研究“晚上喝绿茶与失眠”有无关系,调查了100名人士,得到下面的列联表:
失眠 | 不失眠 | 合计 | |
晚上喝绿茶 | 16 | 40 | 56 |
晚上不喝绿茶 | 5 | 39 | 44 |
合计 | 21 | 79 | 100 |
由已知数据可以求得:![]() ,则根据下面临界值表:
,则根据下面临界值表:
| 0.050 | 0.010 | 0.001 |
| 3.841 | 6.635 | 10.828 |
可以做出的结论是( )
A. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠有关”
B. 在犯错误的概率不超过0.01的前提下认为“晚上喝绿茶与失眠无关”
C. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠有关”
D. 在犯错误的概率不超过0.05的前提下认为“晚上喝绿茶与失眠无关”
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某植物园准备建一个五边形区域的盆栽馆,三角形ABE为盆裁展示区,沿AB、AE修建观赏长廊,四边形BCDE是盆栽养护区,若BCD=∠CDE=120°,∠BAE=60°,DE=3BC=3CD=![]() 米。
米。
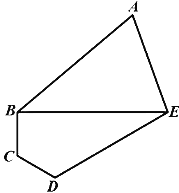
(1)求两区域边界BE的长度;
(2)若区域ABE为锐角三角形,求观赏长廊总长度AB+AE的取值范围。
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com