
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |
| π |
| 3 |
| π |
| 3 |
| π |
| 2 |
| kπ |
| 2 |
| π |
| 12 |
| π |
| 3 |
| π |
| 2 |
| π |
| 3 |
| π |
| 6 |
| π |
| 6 |
| π |
| 3 |
| kπ |
| 2 |
| π |
| 6 |
| π |
| 6 |
| π |
| 2 |


 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案科目:高中数学 来源: 题型:
| 2 |
| π |
| 8 |
| 3 |
| 8 |
| k |
| 2 |
| π |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| π |
| 4 |
| π |
| 8 |
| π |
| 8 |
| 3π |
| 8 |
查看答案和解析>>
科目:高中数学 来源: 题型:
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| k |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
查看答案和解析>>
科目:高中数学 来源: 题型:
已知下表为函数f(x)=ax3+cx+d部分自变量取值及其对应函数值,为便于研究,相关函数值非整数值时,取值精确到0.01.
(1)f(x)为奇函数; (2)f(x)在[0.55,0.6]上必有零点 (3)f(x)在(-∞,-0.35]上单调递减; (4)a<0 其中所有正确命题的个数是( ) |
查看答案和解析>>
科目:高中数学 来源:2014届福建省四地六校高三上学期第一次月考文科数学试卷(解析版) 题型:填空题
关于函数f(x)= 4 sin(2x+ )(
)( ),有下列命题:
),有下列命题:
①由 可得
可得 必是
必是 的整数倍;
的整数倍;
②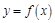 的表达式可改写为
的表达式可改写为 ;
;
③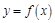 的图象关于点
的图象关于点 对称;
对称;
④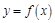 的图象关于直线
的图象关于直线 对称.
对称.
其中正确命题的序号是________________.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com