Question

11．一个直三棱柱被一个平面截后剩余部分的三视图如图，则截去部分的体积与剩余部分的体积之比为（　　）

• A． 1：2
• B． 2：3
• C． 4：5
• D． 5：7

Answer 1

分析 由三视图还原原图形，作出图形，分别利用柱体、台体的体积公式运算求得答案．

解答 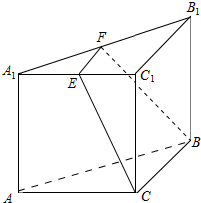解：由三视图还原原几何体如图：
截去的部分为五面体BB₁C₁CEF，剩余的部分为三棱台ACB-A₁EF，
由三视图可知，原直三棱柱底面是边长为2a的等腰直角三角形，
高为2a，
则原直三棱柱的体积为$\frac{1}{2}×2a×2a×2a=4{a}^{3}$，
三棱台的上底面的面积为$\frac{1}{2}{a}^{2}$，下底面的面积为$\frac{1}{2}×2a×2a=2{a}^{2}$，
则三棱台的体积为$\frac{1}{3}×2a（\frac{1}{2}{a}^{2}+\sqrt{\frac{1}{2}{a}^{2}×2{a}^{2}}+2{a}^{2}）$=$\frac{7}{3}{a}^{3}$，
∴截去部分的体积为$4{a}^{3}-\frac{7}{3}{a}^{3}=\frac{5}{3}{a}^{3}$，
则截去部分的体积与剩余部分的体积之比为$\frac{\frac{5}{3}{a}^{3}}{\frac{7}{3}{a}^{3}}$=5：7．
故选：D．

点评 本题考查棱柱、棱锥、棱台的体积，关键是由三视图还原原图形，是中档题．