

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:高中数学 来源: 题型:
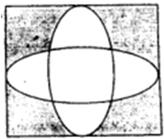 如图,已知正方形的边长为10,向正方形内随机地撒200颗黄豆,数得落在阴影外的黄豆数为114颗,以此实验数据为依据,可以估计出阴影部分的面积约为( )
如图,已知正方形的边长为10,向正方形内随机地撒200颗黄豆,数得落在阴影外的黄豆数为114颗,以此实验数据为依据,可以估计出阴影部分的面积约为( )| A、53 | B、43 | C、47 | D、57 |
查看答案和解析>>
科目:高中数学 来源: 题型:
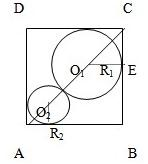 如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.
如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.查看答案和解析>>
科目:高中数学 来源: 题型:
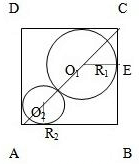 第8题的题干为:如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.
第8题的题干为:如图,已知正方形的边长为1,在正方形ABCD中有两个相切的内切圆.查看答案和解析>>
科目:高中数学 来源:2014届福建省高二上学期期末考试理科数学试卷(解析版) 题型:选择题
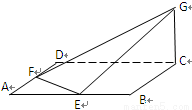
如图,已知正方形 的边长为
的边长为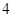 ,
,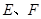 分别是
分别是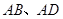 的中点,
的中点,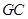 ⊥平面
⊥平面 ,且
,且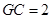 ,则点
,则点 到平面
到平面 的距离为
的距离为
A.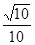 B.
B. C.
C. D.1
D.1
查看答案和解析>>
科目:高中数学 来源:2011-2012学年河北省高三调研理科数学试卷(3) 题型:解答题
如图,已知正方形 的边长为1,
的边长为1, 平面
平面 ,
,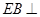 平面
平面 ,
,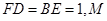 为
为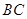 边上的动点。
边上的动点。
(1)证明: 平面
平面 ;
;
(2)试探究点 的位置,使平面
的位置,使平面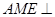 平面
平面 。
。
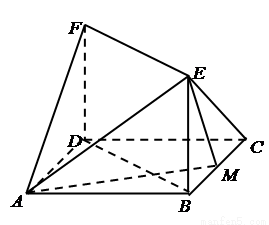
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com