
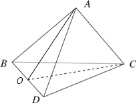
【题目】如图,四面体ABCD中,△ABC是以BC为斜边的等腰直角三角形,△BCD是边长为2的正三角形.

(Ⅰ)当AD为多长时,![]() ?
?
(Ⅱ)当二面角B﹣AC﹣D为![]() 时,求AD的长.
时,求AD的长.
【答案】(Ⅰ)![]() ;(Ⅱ)
;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取BD中点O,连接AO,CO,利用等腰直角三角形与正三角形的性质可得:BD⊥平面AOC,即可得出.
(Ⅱ)如图所示,取BC的中点F,连接DF.利用等腰直角三角形与正三角形的性质可得BC⊥平面ADF.经过D点作DE⊥AF,垂足为E,可得DE⊥平面ABC.假设作EC′⊥AC,垂足为C′.设DE=x,EF=y.可得x2+y2=DF2=3,x=![]() ,解得x=
,解得x=![]() ,y=1.可得点C′与点C重合.可得:∠DCE为二面角B﹣AC﹣D的平面角,即可得出.
,y=1.可得点C′与点C重合.可得:∠DCE为二面角B﹣AC﹣D的平面角,即可得出.
(Ⅰ)取BD中点O,连接AO,CO,
∵△ABC是以BC为斜边的等腰直角三角形,
△BCD是边长为2的正三角形.
∴BC=CD=BD=2,AB=AC=![]() ,
,
∴CO⊥BD,
当AC⊥BD时,由![]() ,得
,得![]() 平面AOC,
平面AOC,
∵![]() 平面AOC,∴
平面AOC,∴![]() ,
,
∴AD=AB=![]() ,
,
∴当AD为![]() 时,
时,![]() .
.
(Ⅱ)如图所示,取BC的中点F,连接DF.
∵△ABC是以BC为斜边的等腰直角三角形,
△BCD是边长为2的正三角形.
∴![]() .又
.又![]() .
.![]() .
.
∴![]() 平面ADF.
平面ADF.
经过D点作![]() ,垂足为E,则DE⊥平面ABC.
,垂足为E,则DE⊥平面ABC.
假设作EC′⊥AC,垂足为C′.
设DE=x,EF=y.
则![]() ,
,![]() ,
,
解得![]() .
.
∴![]() ,因此点C′与点C重合.
,因此点C′与点C重合.
可得![]() 为二面角B﹣AC﹣D的平面角,所以
为二面角B﹣AC﹣D的平面角,所以![]() ,
,
∴![]() .
.


科目:高中数学 来源: 题型:
【题目】设 ![]() ,记不超过x的最大整数为
,记不超过x的最大整数为 ![]() ,令
,令 ![]() ,则
,则  ,
,  ,
, ![]() ( )
( )
A.是等差数列但不是等比数列
B.是等比数列但不是等差数列
C.既是等差数列又是等比数列
D.既不是等差数列也不是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】如图,某小区准备在直角围墙![]() (
(![]() )内建有一个矩形
)内建有一个矩形![]() 的少儿游乐场,
的少儿游乐场,![]() 分别在墙
分别在墙![]() 上,为了安全起见,过矩形的顶点
上,为了安全起见,过矩形的顶点![]() 建造一条如图所示的围栏
建造一条如图所示的围栏![]() ,
,![]() 分别在墙
分别在墙![]() 上,其中,
上,其中,![]() ,
,![]() .
.
(1)①设![]() ,用
,用![]() 表示围栏
表示围栏![]() 的长度;
的长度;
②设![]() ,用
,用![]() 表示围栏
表示围栏![]() 的长度;
的长度;
(2)在第一问中,选择一种表示方法,求如何设计,使得围栏![]() 的长度最小.
的长度最小.

查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修),其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x(单位:m),(1)将y表示为x的函数(2)试确定x , 使修建此矩形场地围墙的总费用最小,并求出最小总费用
(1)将y表示为x的函数:
(2)试确定x , 使修建此矩形场地围墙的总费用最小,并求出最小总费用.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设集合M={x|x2+3x+2<0},集合 ![]() ,则M∪N=( )
,则M∪N=( )
A.{x|x≥﹣2}
B.{x|x>﹣1}
C.{x|x<﹣1}
D.{x|x≤﹣2}
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设f(x)="xln" x–ax2+(2a–1)x,a![]() R.
R.
(Ⅰ)令g(x)=f'(x),求g(x)的单调区间;
(Ⅱ)已知f(x)在x=1处取得极大值.求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ax2+x﹣lnx,(a>0). (Ⅰ)求f(x)的单调区间;
(Ⅱ)设f(x)极值点为x0 , 若存在x1 , x2∈(0,+∞),且x1≠x2 , 使f(x1)=f(x2),求证:x1+x2>2x0 .
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com