
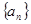 的前n次之和为
的前n次之和为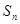 满足
满足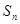 =
=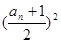
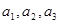 ,
,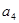 ②猜测数列
②猜测数列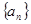 的通项公式,并用数学归纳法加以证明
的通项公式,并用数学归纳法加以证明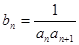 ,数列
,数列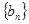 的前n项和为
的前n项和为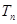 ,求
,求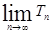 的值.
的值. 全优考典单元检测卷及归类总复习系列答案
全优考典单元检测卷及归类总复习系列答案科目:高中数学 来源:不详 题型:解答题
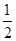 an-1+1 (n≥2)
an-1+1 (n≥2) 查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
 }的前n项和Sn= —a
}的前n项和Sn= —a —(
—( )
)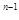 +2 (n为正整数).
+2 (n为正整数). =
= a
a + (
+ ( )
) .,并求数列{a
.,并求数列{a }的通项
}的通项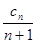 =
=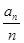 ,T
,T = c
= c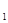 +c
+c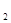 +···+c
+···+c ,求T
,求T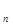 .
.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com