练习册

  • 练习册
  • 试题
    精英家教网 > 高中数学 > 题目详情

    【题目】已知二次函数有两个零点0和-2，且最小值是-1，函数与的图象关于原点对称．

    （1）求和的解析式；

    （2）若在区间上是增函数，求实数的取值范围．

    【答案】（1）,；（2）.

    【解析】

    试题分析：（1）依题意，设，对称轴是，所以，所以，即.与关于原点对称，所以.（2）化简，当时，满足在区间上是增函数；当时，函数开口向下，只需对称轴大于或等于；当时，函数开口向上，只需对称轴小于或等于.综上求得实数的取值范围．

    试题解析：

    （1）依题意，设，对称轴是，

    ∴，∴，∴

    由函数与的图象关于原点对称，

    ∴

    （2）由（1）得

    ①当时，满足在区间上是增函数；

    ②当时，图象在对称轴是，则，

    又∵，解得

    ③当时，有，又∵，解得

    综上所述，满足条件的实数的取值范围是

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：高中数学 来源： 题型：

    【题目】已知函数.

    （Ⅰ）当时，求证：函数的图像关于点对称；

    （Ⅱ）当时，求的单调区间.

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知l⊥平面α，直线m平面β.有下面四个命题：
    ①α∥βl⊥m；②α⊥βl∥m；③l∥mα⊥β；④l⊥mα∥β.
    其中正确的命题是（ ）
    A.①②
    B.③④
    C.②④
    D.①③

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】如图，四棱锥P﹣ABCD的底面是边长为1的正方形，PA⊥底面ABCD，E、F分别为AB、PC的中点．

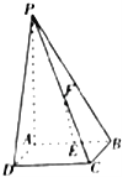
    （Ⅰ）求证：EF∥平面PAD；

    （Ⅱ）若PA=2，试问在线段EF上是否存在点Q，使得二面角Q﹣AP﹣D的余弦值为？若存在，确定点Q的位置；若不存在，请说明理由．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】小明中午放学回家自己煮面条吃,有下面几道工序:①洗锅盛水2分钟;②洗菜6分钟;③准备面条及佐料2分钟;④用锅把水烧开10分钟;⑤煮面条和菜共3分钟.以上各道工序,除了④之外,一次只能进行一道工序.小明要将面条煮好,最少要用(　　)

    A. 13分钟 B. 14分钟

    C. 15分钟 D. 23分钟

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】（）．

    （1）当时，求的单调区间；

    （2）若，存在两个极值点，，试比较与的大小；

    （3）求证：（，）．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】设平面直角坐标系原点与极坐标极点重合，x轴正半轴与极轴重合，若已知曲线C的极坐标方程为，点F1、F2为其左、右焦点，直线l的参数方程为（t为参数，t∈R）．

    （Ⅰ）求曲线C的标准方程和直线l的普通方程；

    （Ⅱ）若点P为曲线C上的动点，求点P到直线l的最大距离．

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】下列条件中，能使直线m⊥平面α的是（ ）
    A.m⊥b，m⊥c，bα，cα
    B.m⊥b，b∥α
    C.m∩b＝A，b⊥α
    D.m∥b，b⊥α

    查看答案和解析>>

    科目：高中数学 来源： 题型：

    【题目】已知点，圆是以的中点为圆心， 为半径的圆.

    （Ⅰ）若圆的切线在轴和轴上截距相等，求切线方程；

    （Ⅱ）若是圆外一点，从向圆引切线， 为切点， 为坐标原点，且有，求使最小的点的坐标.

    查看答案和解析>>

    同步练习册答案