
���� ��1�����ݡ����������͡����������Ķ��壬�����жϼ��ɣ�
��2�������������Ķ��壬�������Ϲ�ϵ������⼴�ɣ�
��3�����ݳ�������ͱ�Ҫ�����Ķ����ϡ�α���������Ķ��������⼴�ɣ�
��� �⣺��1���������f��x��=tanx�Ķ�����A={x|x��$\frac{��}{2}$+k�У�k��Z}��ֵ��B=��-�ޣ�+�ޣ�������A?B����f��x����A��Ϊ��������������2�֣�
��2��$f��x��=lnx-\frac{a}{x}$��[1��e]���ǡ����������ȼ���f��x���Ķ�����A�������ֵ��B��
f�䣨x��=$\frac{1}{x}$+$\frac{a}{{x}^{2}}$
��f�䣨x��=0�����x=-a��
�б��ɵ�f��x���ڣ�0��-a���ϵ���������-a��+�ޣ��ϵ�������
1�㵱-a��1����a��-1ʱ����x��[1��e]����f'��x����0���������f��x����[1��e]����������
�ɵ�f��x��min=f��1��=-a��f��x��max=f��e��=1-$\frac{a}{e}$��
�ɡ����������Ķ����֪��$\left\{{\begin{array}{l}{f��1��=-a��1}\\{f��e��=1-\frac{a}{e}��e}\end{array}}\right.$���ҡ�=����ͬʱ������
��$\left\{{\begin{array}{l}{a��-1}\\{a��e-{e^2}}\end{array}}\right.$����Ȼ����ʽ���⣮����4�֣���
2�㵱a��-eʱ��
��x��[1��e]����f'��x����0���������f��x����x��[1��e]�����ݼ���
��$f{��x��_{min}}=f��e��=1-\frac{a}{e}��f{��x��_{max}}=f��1��=-a$��
�ɡ����������Ķ����֪��$\left\{{\begin{array}{l}{f��1��=-a��e}\\{f��e��=1-\frac{a}{e}��1}\end{array}}\right.$���ҡ�=����ͬʱ������
��$\left\{{\begin{array}{l}{a��-e}\\{a��0}\end{array}}\right.$������Ϊa��-e�����Բ���ʽ�����⣮����6�֣�
3�㵱-e��a��-1ʱ��
��x�ʣ�1��-a��ʱ��f�䣨x����0����x�ʣ�-a��e��ʱ��f�䣨x����0��
��f��-a��Ϊ��Сֵ��������[1��e]�ϣ�f��-a��Ϊ��Сֵ�����ֵΪf��1����f��e��
�ɡ����������Ķ����֪��$\left\{{\begin{array}{l}{f��{-a}����1}\\{f��1����e}\\{f��e����e}\end{array}}\right.$$⇒\left\{{\begin{array}{l}{ln��{-a}��+1��1}\\{-a��e}\\{1-\frac{a}{e}��e}\end{array}}\right.$$⇒\left\{{\begin{array}{l}{a��-1}\\{a��-e}\\{a��e-{e^2}}\end{array}}\right.$��
����������ã�-e��a��-1����8�֣�
�����飬��a=-e��a=-1ʱ��A��B����
���Ͽɵõã�a�ķ�ΧΪ[-e��-1]����10�֣�
��3������ԣ�
��f��x����������a�ĺ���h��a������Ȼ���ǹ���a��һԪһ�κ�����
��x��1����h��a��������������a��1����f��x��=ax-lnx��x-lnx��
��֤x-lnx��1��
��g��x��=x-lnx��${g^'}��x��=1-\frac{1}{x}$����x��[1��+�ޣ���g�䣨x����0��x��[1��+�ޣ�ʱ��g��x������������
��g��x��min=g��1��=1��
��g��x����1����x-lnx��1��
��f��x����[1��+�ޣ����������ô��ȻB⊆A����14�֣�
��Ҫ�ԣ�
f��x����[1��+�ޣ��ǡ�α����������
��f��x����1��[1��+�ޣ��������
��x=1ʱ��f��1��=a��1����a��1����16�֣�
֤��
���� ������Ҫ�����뺯���йص����������жϺ�Ӧ�ã����ݶ����ϼ��Ϲ�ϵ�ǽ������Ĺؼ���



| �꼶 | ���пγ� | �꼶 | ���пγ� |
| ��һ | ��һ��ѿγ��Ƽ��� | ��һ | ��һ��ѿγ��Ƽ��� |
| �߶� | �߶���ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
| ���� | ������ѿγ��Ƽ��� | ���� | ������ѿγ��Ƽ��� |
��Ŀ��������ѧ ��Դ�� ���ͣ������
 һ��ʯ�ı�ʾ�ļ����������ͼ��ͼ��ʾ������ʯ����������ĥ���ӹ��������ܵõ��������İ뾶����2��
һ��ʯ�ı�ʾ�ļ����������ͼ��ͼ��ʾ������ʯ����������ĥ���ӹ��������ܵõ��������İ뾶����2���鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ�ѡ����
| A�� | -48 | B�� | -50 | C�� | -52 | D�� | -49 |
�鿴�𰸺ͽ���>>
��Ŀ��������ѧ ��Դ�� ���ͣ������
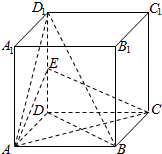 ��ͼ����������ABCD-A1B1C1D1�У�EΪDD1���е㣮
��ͼ����������ABCD-A1B1C1D1�У�EΪDD1���е㣮�鿴�𰸺ͽ���>>
����ʡ������Υ���Ͳ�����Ϣ�ٱ�ƽ̨ | �����к���Ϣ�ٱ�ר�� | ����թƭ�ٱ�ר�� | ����ʷ���������к���Ϣ�ٱ�ר�� | ������Ȩ�ٱ�ר��
Υ���Ͳ�����Ϣ�ٱ��绰��027-86699610 �ٱ����䣺58377363@163.com