D
分析:根据电路的知识,按1、4的闭合与否,分三种情况讨论:(1)若1闭合,而4不闭合,(2)若4闭合,而1不闭合,(3)若1、4都闭合,分别求出每种情况下的电路接通的情况数目,由分类计数原理计算可得答案.
解答:若电路从P到Q接通,有三种情况:
(1)若1闭合,而4不闭合,
具体有:①若1、2闭合,而4不闭合,则3、5可以闭合也可以不闭合,有2×2=4种情况,
②若1、3、5闭合,而4不闭合,则2可以闭合也可以不闭合,有2种情况,
但①与②中都包含1、2、3、5都闭合,而4不闭合的情况,则(1)中有4+2-1=5种情况;
(2)若4闭合,而1不闭合,
③若4、5闭合,而1不闭合,则2、3可以闭合也可以不闭合,有2×2=4种情况;
④若4、3、2闭合,而1不闭合,则5可以闭合也可以不闭合,有2种情况;
但④与⑤中都包含4、2、3、5都闭合,而1不闭合的情况,则(2)中有4+2-1=5种情况;
(3)若1、4都闭合,共有2×2×2=8种情况,
而其中电路不通的有2、3、5都不闭合与2、5都不闭合2种情况;
则此时电路接通的情况有8-2=6种;
故电路接通的情况有5+5+6=16种,
故选D.
点评:本题考查分类计数原理的运用,注意结合物理知识,正确分析电路.

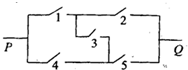
 如图所示的每个开关都有闭合与不闭合两种可能,因此5个开关共有25种可能,在这25种可能中电路从P到Q接通的情况有
如图所示的每个开关都有闭合与不闭合两种可能,因此5个开关共有25种可能,在这25种可能中电路从P到Q接通的情况有


 云南师大附小一线名师提优作业系列答案
云南师大附小一线名师提优作业系列答案