
 (其中ω>0,a∈R).且f(x)的图象在y轴右侧的第一个最高点的横坐标是
(其中ω>0,a∈R).且f(x)的图象在y轴右侧的第一个最高点的横坐标是 .
. 上的最小值为
上的最小值为 ,求a的值.
,求a的值.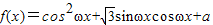 ,利用二倍角公式和辅助角公式,我们易将函数的解析式化简成正弦型函数的形式,再由f(x)的图象在y轴右侧的第一个最高点的横坐标是
,利用二倍角公式和辅助角公式,我们易将函数的解析式化简成正弦型函数的形式,再由f(x)的图象在y轴右侧的第一个最高点的横坐标是 .构造关于ω的方程,解方程即可求出ω的值;
.构造关于ω的方程,解方程即可求出ω的值;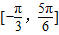 上的单调性,结合f(x)在区间
上的单调性,结合f(x)在区间 上的最小值为
上的最小值为 ,构造关于a的方程,解方程即可求出a的值.
,构造关于a的方程,解方程即可求出a的值.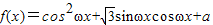 =
=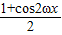 +
+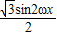 +a
+a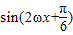 +
+ +a------3分
+a------3分 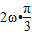 +
+ =
=
 -------------------5分
-------------------5分 
 )+
)+ +a.
+a. 时,
时, ∈
∈ sinx∈
sinx∈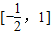 ,
,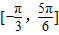 上的最小值为
上的最小值为 +
+ +a,故a=
+a,故a=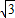


科目:高中数学 来源: 题型:
| π |
| 6 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:不详 题型:解答题
| π |
| 6 |
| π |
| 2 |
查看答案和解析>>
科目:高中数学 来源:2011-2012学年江苏省苏州市高一(上)期末数学复习试卷4(解析版) 题型:解答题
 ,其中a>0.若函数f(x)与g(x)的图象有且只有一个交点,求a的取值范围.
,其中a>0.若函数f(x)与g(x)的图象有且只有一个交点,求a的取值范围.查看答案和解析>>
科目:高中数学 来源:2011-2012学年湖北省黄陂一中高三(上)7月滚动检测数学试卷(1)(解析版) 题型:解答题
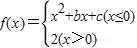 ,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.
,其中b>0,c∈R.当且仅当x=-2时,函数f(x)取得最小值-2.查看答案和解析>>
科目:高中数学 来源:2010-2011学年江苏省徐州市高三上学期阶段性检测数学试卷 题型:解答题
(本小题满分16分)
设函数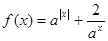 (其中常数
(其中常数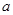 >0,且
>0,且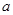 ≠1).
≠1).
(Ⅰ)当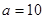 时,解关于
时,解关于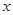 的方程
的方程 (其中常数
(其中常数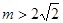 );
);
(Ⅱ)若函数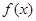 在
在 上的最小值是一个与
上的最小值是一个与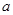 无关的常数,求实数
无关的常数,求实数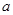 的取值范围.
的取值范围.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com