
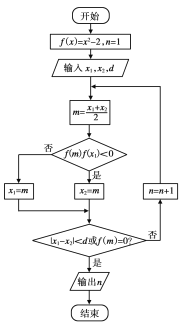
【题目】二分法是求方程近似解的一种方法,其原理是“一分为二、无限逼近”.执行如图所示的程序框图,若输入![]() ,则输出
,则输出![]() 的值( )
的值( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
【答案】B
【解析】模拟程序的运行,可得
n=1,x1=1,x2=2,d=0.1,
令f(x)=x22,则f(1)=1<0,f(2)=2>0,
m=1.5,f(1.5)=0.25>0,满足条件f(m)f(x1)<0,x2=1.5,
此时|1.51|=0.5>0.05,不合精确度要求。
n=2,m=1.25,f(1.25)=0.4375<0.不满足条件f(m)f(x1)<0,x1=1.25,
此时|1.51.25|=0.25>0.05,不合精确度要求。
n=3,m=1.375,f(1.375)=0.109<0.不满足条件f(m)f(x1)<0,x1=1.375,
此时|1.51.375|=0.125>0.05,不合精确度要求。
n=4,m=1.375,f(1.4375)=0.066>0.满足条件f(m)f(x1)<0,x2=1.4375,此时|1.51.4375|=0.062>0.05,符合精确度要求。
n=5,m=1.4375,f(1.40625)=0.066<0.满足条件f(m)f(x1)<0,x1=1.40625,此时|1.51.4375|=0.03125<0.05,符合精确度要求。
退出循环,输出n的值为5.
本题选择B选项.


 小学学习好帮手系列答案
小学学习好帮手系列答案 小学同步三练核心密卷系列答案
小学同步三练核心密卷系列答案科目:高中数学 来源: 题型:
【题目】从某企业生产的产品中抽取1000件测量这些产品的一项质量指标值,由测量结果得到频率分布直方图如图所示.
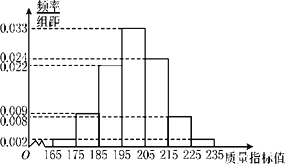
(Ⅰ)求这1000件产品质量指标值的样本平均数![]() 和样本方差s2(同一组数据用该区间的中点值作代表).
和样本方差s2(同一组数据用该区间的中点值作代表).
(Ⅱ)由频率分布直方图可以认为这种产品的质量指标值Z服从正态分布N(μ,δ2),其中μ近似为样本平均数![]() ,δ2近似为样本方差s2.
,δ2近似为样本方差s2.
![]() 利用该正态分布,求P(175.6<Z<224.4);
利用该正态分布,求P(175.6<Z<224.4);
②某用户从该企业购买了100件这种产品,估计其中质量指标值位于区间(175.6,224.4)的产品件数.(精确到个位)
附: ![]() ≈12.2,若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,
≈12.2,若Z~N(μ,δ2),则P(μ-δ<Z<μ+δ)=0.6826,
P(μ-2δ<Z<μ+2δ)=0.9544
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数![]() 定义在
定义在![]() 上的奇函数,
上的奇函数, ![]() 的最大值为
的最大值为![]() .
.
(1)求函数![]() 的解析式;
的解析式;
(2)关于![]() 的方程
的方程![]() 在
在![]() 上有解,求实数
上有解,求实数![]() 的取值范围;
的取值范围;
(3)若存在![]() ,不等式
,不等式![]() 成立,请同学们探究实数
成立,请同学们探究实数![]() 的所有可能取值.
的所有可能取值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】用另一种方法表示下列集合.
(1){x||x|≤2,x∈Z};
(2){能被3整除,且小于10的正数};
(3)坐标平面内在第四象限的点组成的集合.
(4){(x,y)|x+y=6,x,y均为正整数};
(5){-3,-1,1,3,5}.
(6)被3除余2的正整数集合.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】设![]() :实数
:实数![]() 满足不等式
满足不等式![]() ,
, ![]() :函数
:函数![]() 无极值点.
无极值点.
(1)若“![]() ”为假命题,“
”为假命题,“![]() ”为真命题,求实数
”为真命题,求实数![]() 的取值范围;
的取值范围;
(2)已知“![]() ”为真命题,并记为
”为真命题,并记为![]() ,且
,且![]() :
: ![]() ,若
,若![]() 是
是![]() 的必要不充分条件,求正整数
的必要不充分条件,求正整数![]() 的值.
的值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知f(x)是定义在R上的偶函数,且x≤0时,f(x)=log![]() (-x+1).
(-x+1).
(1)求f(0),f(1);
(2)求函数f(x)的解析式;
(3)若f(a-1)<-1,求实数a的取值范围.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某车间20名工人年龄数据如下表:
年龄(岁) | 19 | 24 | 26 | 30 | 34 | 35 | 40 | 合计 |
工人数(人) | 1 | 3 | 3 | 5 | 4 | 3 | 1 | 20 |
(1)求这20名工人年龄的众数与平均数;
(2)以十位数为茎,个位数为叶,作出这20名工人年龄的茎叶图;
(3)从年龄在24和26的工人中随机抽取2人,求这2人均是24岁的概率.
查看答案和解析>>
科目:高中数学 来源: 题型:
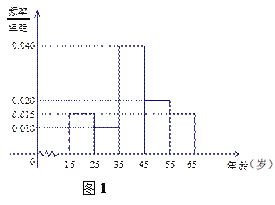
【题目】电视连续剧《人民的名义》自2017年3月28日在湖南卫视开播以来,引发各方关注,收视率、点击率均占据各大排行榜首位.我们用简单随机抽样的方法对这部电视剧的观看情况进行抽样调查,共调查了600人,得到结果如下:其中图1是非常喜欢《人民的名义》这部电视剧的观众年龄的频率分布直方图;表1是不同年龄段的观众选择不同观看方式的人数.
观看方式 年龄(岁) | 电视 | 网络 |
| 150 | 250 |
| 120 | 80 |
![]()
求:(I)假设同一组中的每个数据用该组区间的中点值代替,求非常喜欢《人民的名义》这部电视剧的观众的平均年龄;
(II)根据表1,通过计算说明我们是否有99%的把握认为观看该剧的方式与年龄有关?
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
附: 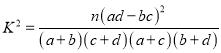
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com