
分析 (1)设等差数列{an}的公差为d,则依题设可得d=2,a1=1,从而能够得到数列{an}的通项公式;
(2)因为bn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),利用列项相消法求和即可,再利用放缩即可证明.
解答 解:(1)设等差数列{an}的公差为d,则依题设d>0
由a2+a7=16.得2a1+7d=16①
由a3•a6=55,得(a1+2d)(a1+5d)=55②
由①得2a1=16-7d,将其代入②得(16-3d)(16+3d)=220,
即256-9d2=220,
9d2=36,解得:d=±2,
又{an}是一个大于0的等差数列,
因此d=-2不符合题意舍去,所以d=2,代入①得a1=1,
所以an=1+2(n-1)=2n-1;
(2)因为bn=$\frac{1}{{a}_{n}{a}_{n+1}}$=$\frac{1}{(2n-1)(2n+1)}$=$\frac{1}{2}$($\frac{1}{2n-1}$-$\frac{1}{2n+1}$),
所以Tn=$\frac{1}{2}$(1-$\frac{1}{3}$+$\frac{1}{3}$-$\frac{1}{5}$+…+$\frac{1}{2n-1}$-$\frac{1}{2n+1}$)=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)=$\frac{n}{2n+1}$
所以Tn=$\frac{1}{2}$(1-$\frac{1}{2n+1}$)<$\frac{1}{2}$,
当n=1时,Tn=$\frac{1}{4}$
所以Tn的取值范围[$\frac{1}{4}$,$\frac{1}{2}$)
点评 本题考查数列的求和,着重考查等差数列的通项公式与列项相消法求和以及放缩法,考查运算求解能力,属于中档题.


科目:高中数学 来源: 题型:解答题
查看答案和解析>>
科目:高中数学 来源: 题型:解答题
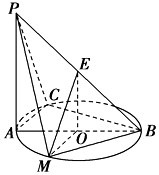 如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.
如图所示,PA⊥平面ABC,点C在以AB为直径的⊙O上,∠CBA=30°,PA=AB=2,点E为线段PB的中点,点M在$\widehat{AB}$上,且OM∥AC.查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | [0,+∞) | B. | [2,+∞) | C. | [$\frac{1}{2}$,+∞) | D. | [$\frac{1}{2}$,$\frac{5}{2}$) |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | z的实部为-$\frac{1}{2}$ | B. | z的虚部为-$\frac{1}{2}$i | ||
| C. | |z|=$\frac{1}{2}$ | D. | z的共轭复数为$\frac{1}{2}$+$\frac{1}{2}$i |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | 45 | B. | 46 | C. | 47 | D. | 48 |
查看答案和解析>>
科目:高中数学 来源: 题型:选择题
| A. | f(x1)<0,f(x2)<0 | B. | f(x1)<0,f(x2)>0 | C. | f(x1)>0,f(x2)<0 | D. | f(x1)>0,f(x2)>0 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com