
【题目】已知函数![]() .
.
(1)求不等式![]() 的解集;
的解集;
(2)若直线![]() 与
与![]() 的图象所围成的多边形面积为
的图象所围成的多边形面积为![]() ,求实数
,求实数![]() 的值.
的值.
【答案】(1) ![]() (2)4
(2)4
【解析】
(Ⅰ)去掉绝对值号,得到分段函数,分类讨论即可求解不等式的解集,得到答案;
(Ⅱ)画出函数![]() 的图象,得出直线
的图象,得出直线![]() 与函数
与函数![]() 围成的图形,利用梯形的面积公式,即可求解.
围成的图形,利用梯形的面积公式,即可求解.
(Ⅰ)由题意,可得函数f(x)=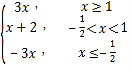 ,
,
由f(x)≥3可知:
(i)当x≥1时,3x≥3,即x≥1;
(ii)当-![]() <x<1时,x+2>3,即x≥1,与-
<x<1时,x+2>3,即x≥1,与-![]() <x<1矛盾,舍去;
<x<1矛盾,舍去;
(iii)当x≤-![]() 时,-3x≥3,即x≤-1;
时,-3x≥3,即x≤-1;
综上可知解集为{x|x≤-1或x≥1}.
(Ⅱ)画出函数y=f(x)的图象,如图所示,其中A(-![]() ,
,![]() ),B(1,3),
),B(1,3),
由kAB=1,知y=x+a图象与直线AB平行,若要围成多边形,则a>2.
易得y=x+a与y=f(x)图象交于两点C(![]() ,
,![]() ),D(-
),D(-![]() ,
,![]() ),则|CD|=
),则|CD|=![]() |
|![]() +
+![]() |=
|=![]() a.
a.
平行线AB与Cd间的距离d=![]() =
=![]() ,且|AB|=
,且|AB|=![]() ,
,
∴梯形ABCDspan>的面积S=![]()
![]() =
=![]() (a-2)=
(a-2)=![]() ,(a>2).
,(a>2).
即(a+2-(a-2)=12,∴a=4,
故所求实数a的值为4.
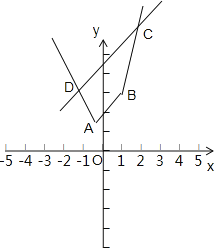


 名校课堂系列答案
名校课堂系列答案科目:高中数学 来源: 题型:
【题目】已知椭圆![]() 经过点
经过点 .离心率
.离心率![]() .
.
(1)求椭圆C的标准方程;
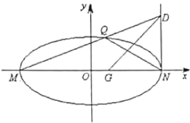
(2)若M,N分别是椭圆长轴的左、右端点,动点D满足![]() ,连接MD交椭圆于点Q.问:x轴上是否存在异于点M的定点G,使得以QD为直径的圆恒过直线QN,GD的交点?若存在,求出点G的坐标;若不存在,说明理由.
,连接MD交椭圆于点Q.问:x轴上是否存在异于点M的定点G,使得以QD为直径的圆恒过直线QN,GD的交点?若存在,求出点G的坐标;若不存在,说明理由.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知平面内一动点![]() (
(![]() )到点
)到点![]() 的距离与点
的距离与点![]() 到
到![]() 轴的距离的差等于1,
轴的距离的差等于1,
(1)求动点![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(2)过点![]() 的直线
的直线![]() 与轨迹
与轨迹![]() 相交于不同于坐标原点
相交于不同于坐标原点![]() 的两点
的两点![]() ,求
,求![]() 面积的最小值.
面积的最小值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某不透明纸箱中共有4个小球,其中1个白球,3个红球,它们除颜色外均相同.
(Ⅰ)一次从纸箱中摸出两个小球,求恰好摸出2个红球的概率;
(Ⅱ)每次从纸箱中摸出一个小球,记录颜色后放回纸箱,这样摸取4次,记得到红球的次数为![]() ,求
,求![]() 的分布列;
的分布列;
(Ⅲ)每次从纸箱中摸出一个小球,记录颜色后放回纸箱,这样摸取100次,得到几次红球的概率最大?只需写出结论.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知表1和表2是某年部分日期的天安门广场升旗时刻表.
表1:某年部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
1月1日 | 7:36 | 4月9日 | 5:46 | 7月9日 | 4:53 | 10月8日 | 6:17 |
1月21日 | 7:31 | 4月28日 | 5:19 | 7月27日 | 5:07 | 10月26日 | 6:36 |
2月10日 | 7:14 | 5月16日 | 4:59 | 8月14日 | 5:24 | 11月13日 | 6:56 |
3月2日 | 6:47 | 6月3日 | 4:47 | 9月2日 | 5:42 | 12月1日 | 7:16 |
3月22日 | 6:15 | 6月22日 | 4:46 | 9月20日 | 5:59 | 12月20日 | 7:31 |
表2:某年2月部分日期的天安门广场升旗时刻表
日期 | 升旗时刻 | 日期 | 升旗时刻 | 日期 | 升旗时刻 |
2月1日 | 7:23 | 2月11日 | 7:13 | 2月21日 | 6:59 |
2月3日 | 7:22 | 2月13日 | 7:11 | 2月23日 | 6:57 |
2月5日 | 7:20 | 2月15日 | 7:08 | 2月25日 | 6:55 |
2月7日 | 7:17 | 2月17日 | 7:05 | 2月27日 | 6:52 |
2月9日 | 7:15 | 2月19日 | 7:02 | 2月28日 | 6:49 |
(Ⅰ)从表1的日期中随机选出一天,试估计这一天的升旗时刻早于7:00的概率;
(Ⅱ)甲,乙二人各自从表2的日期中随机选择一天观看升旗,且两人的选择相互独立.记![]() 为这两人中观看升旗的时刻早于7:00的人数,求
为这两人中观看升旗的时刻早于7:00的人数,求![]() 的分布列和数学期望
的分布列和数学期望![]() .
.
(Ⅲ)将表1和表2中的升旗时刻化为分数后作为样本数据(如7:31化为![]() ).记表2中所有升旗时刻对应数据的方差为
).记表2中所有升旗时刻对应数据的方差为![]() ,表1和表2中所有升旗时刻对应数据的方差为
,表1和表2中所有升旗时刻对应数据的方差为![]() ,判断
,判断![]() 与
与![]() 的大小.(只需写出结论)
的大小.(只需写出结论)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】国家统计局进行第四次经济普查,某调查机构从15个发达地区,10个欠发达地区,5个贫困地区中选取6个作为国家综合试点地区,然后再逐级确定普查区域,直到基层的普查小区.普查过程中首先要进行宣传培训,然后确定对象,最后入户登记,由于种种情况可能会导致入户登记不够顺利,这为正式普查提供了宝贵的试点经验,在某普查小区,共有50家企事业单位,150家个体经营户,普查情况如下表所示:
普查对象类别 | 顺利 | 不顺利 | 合计 |
企事业单位 | 40 | 10 | 50 |
个体经营户 | 90 | 60 | 150 |
合计 | 130 | 70 | 200 |
(1)写出选择6个国家综合试点地区采用的抽样方法;
(2)根据列联表判断是否有97.5%的把握认为“此普查小区的入户登记是否顺利与普查对象的类别有关”,分析造成这个结果的原因并给出合理化建议.
附:参考公式:![]() ,其中
,其中![]()
参考数据:
| 0.50 | 0.40 | 0.25 | 0.15 | 0.10 | 0.05 | 0.025 |
| 0.455 | 0.708 | 1.323 | 2.072 | 2.706 | 3.841 | 5.024 |
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某网站针对“2014年法定节假日调休安排”展开的问卷调查,提出了A、B、C三种放假方案,调查结果如下:
支持A方案 | 支持B方案 | 支持C方案 | |
35岁以下 | 200 | 400 | 800 |
35岁以上(含35岁) | 100 | 100 | 400 |
(1)在所有参与调查的人中,用分层抽样的方法抽取n个人,已知从“支持A方案”的人中抽取了6人,求n的值;
(2)在“支持B方案”的人中,用分层抽样的方法抽取5人看作一个总体,从这5人中任意选取2人,求恰好有1人在35岁以上(含35岁)的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com