
【题目】为了了解居民的家庭收人情况,某社区组织工作人员从该社区的居民中随机抽取了![]() 户家庭进行问卷调查.经调查发现,这些家庭的月收人在
户家庭进行问卷调查.经调查发现,这些家庭的月收人在![]() 元到
元到![]() 元之间,根据统计数据作出如图所示的频率分布直方图.已知图中从左至右第一 、二、四小组的频率之比为
元之间,根据统计数据作出如图所示的频率分布直方图.已知图中从左至右第一 、二、四小组的频率之比为![]() ,且第四小组的频数为
,且第四小组的频数为![]() .
.
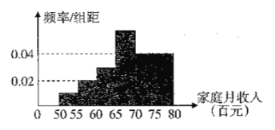
(1)求![]() ;
;
(2)求这![]() 户家庭月收人的众数与中位数(结果精确到
户家庭月收人的众数与中位数(结果精确到![]() );
);
(3)这![]() 户家庭月收入在第一、二、三小组的家庭中,用分层抽样的方法任意抽取
户家庭月收入在第一、二、三小组的家庭中,用分层抽样的方法任意抽取![]() 户家庭,并从这
户家庭,并从这![]() 户家庭中随机抽取
户家庭中随机抽取![]() 户家庭进行慰问,求这
户家庭进行慰问,求这![]() 户家庭月收入都不超过
户家庭月收入都不超过![]() 元的概率.
元的概率.
【答案】(1)![]() (2)众数是67.5,中位数是66.3 (3)
(2)众数是67.5,中位数是66.3 (3)![]()
【解析】
(1)根据从左至右第一 、二、四小组的频率之比为![]() ,求出第四小组的频率,再由频率
,求出第四小组的频率,再由频率![]() 即可求解.
即可求解.
(2)由频率分布直方图第四组小矩形底边中点的横坐标为众数;中位数等于各个小矩形面积与其小矩形底边中点横坐标之积的和.
(3)根据分层抽样得出第一、二、三小组应分别抽取![]() ,分别记记为
,分别记记为![]()
依次列出基本事件个数,由古典概型的概率求法公式即可求解.
解:(Ⅰ)设从左至右第一、三、四小组的频率分别为![]() ,则由题意可知:
,则由题意可知:
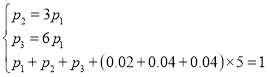 ,解得
,解得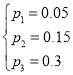
从而![]()
(2)由于第四小组频率最大,故这 ![]() 户家庭月收入的众数为
户家庭月收入的众数为![]()
由于前四小组的频率之和为:![]()
故这![]() 户家庭月收入的中位数应落在第四小组,设中位数为
户家庭月收入的中位数应落在第四小组,设中位数为 ![]()
则![]() ,解得
,解得![]()
(3)因为家庭月收入在第一、二、三小组的家庭分别有![]() 户,按照分层抽样的方法易知分别抽取
户,按照分层抽样的方法易知分别抽取![]() ,第一组记为
,第一组记为![]() ,第二组
,第二组![]() ,第三组为
,第三组为![]() ,
,
从中随机抽取2 户家庭的方法共有![]()
![]() 共
共![]() 种;
种;
其中这![]() 户家庭月收入都不超过
户家庭月收入都不超过![]() 元的有
元的有
![]()
![]() 共
共![]() 种;
种;
所以这![]() 户家庭月收入都不超过
户家庭月收入都不超过![]() 元的概率为
元的概率为![]()


科目:高中数学 来源: 题型:
【题目】用一个长为![]() ,宽为
,宽为![]() 的矩形铁皮(如图1)制作成一个直角圆形弯管(如图3):先在矩形的中间画一条曲线,并沿曲线剪开,将所得的两部分分别卷成体积相等的斜截圆柱状(如图2),然后将其中一个适当翻转拼接成直角圆形弯管(如图3)(不计拼接损耗部分),并使得直角圆形弯管的体积最大;
的矩形铁皮(如图1)制作成一个直角圆形弯管(如图3):先在矩形的中间画一条曲线,并沿曲线剪开,将所得的两部分分别卷成体积相等的斜截圆柱状(如图2),然后将其中一个适当翻转拼接成直角圆形弯管(如图3)(不计拼接损耗部分),并使得直角圆形弯管的体积最大;
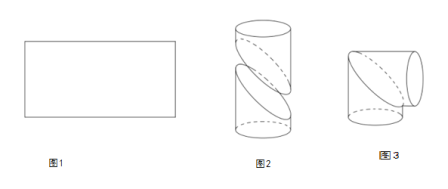
(1)求直角圆形弯管(图3)的体积;
(2)求斜截面椭圆的焦距;
(3)在相应的图1中建立适当的坐标系,使所画的曲线的方程为![]() ,求出方程并画出大致图像;
,求出方程并画出大致图像;
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知椭圆![]() :
:![]() 的一个焦点为
的一个焦点为![]() ,离心率为
,离心率为![]() .
.
(1)求![]() 的标准方程;
的标准方程;
(2)若动点![]() 为
为![]() 外一点,且
外一点,且![]() 到
到![]() 的两条切线相互垂直,求
的两条切线相互垂直,求![]() 的轨迹
的轨迹![]() 的方程;
的方程;
(3)设![]() 的另一个焦点为
的另一个焦点为![]() ,过
,过![]() 上一点
上一点![]() 的切线与(2)所求轨迹
的切线与(2)所求轨迹![]() 交于点
交于点![]() ,
,![]() ,求证:
,求证:![]() .
.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】实数a,b满足ab>0且a≠b,由a、b、![]() 、
、![]() 按一定顺序构成的数列( )
按一定顺序构成的数列( )
A. 可能是等差数列,也可能是等比数列
B. 可能是等差数列,但不可能是等比数列
C. 不可能是等差数列,但可能是等比数列
D. 不可能是等差数列,也不可能是等比数列
查看答案和解析>>
科目:高中数学 来源: 题型:
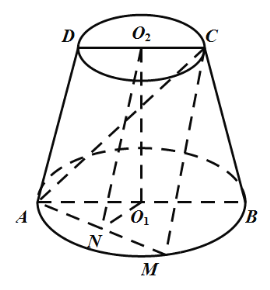
【题目】如图,在圆台![]() 中,平面
中,平面![]() 过上下底面的圆心
过上下底面的圆心![]() ,
,![]() ,点M在
,点M在![]() 上,N为
上,N为![]() 的中点,
的中点,![]() .
.
(1)求证:平面![]() 平面
平面![]() ;
;
(2)当![]() 时,
时,![]() 与底面
与底面![]() 所成角的正弦值为
所成角的正弦值为![]() ,求二面角
,求二面角![]() 的余弦值.
的余弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
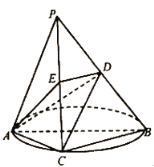
【题目】如图,![]() 是一个三棱锥,
是一个三棱锥,![]() 是圆的直径,
是圆的直径,![]() 是圆上的点,
是圆上的点,![]() 垂直圆所在的平面,
垂直圆所在的平面,![]() ,
,![]() 分别是棱
分别是棱![]() ,
,![]() 的中点.
的中点.
(1)求证:![]() 平面
平面![]() ;
;
(2)若二面角![]() 是
是![]() ,
,![]() ,求
,求![]() 与平面
与平面![]() 所成角的正弦值.
所成角的正弦值.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为了鼓励职员工作热情,某公司对每位职员一年来的工作业绩按月进行考评打分;年终按照职员的月平均值评选公司最佳职员并给予相应奖励.已知职员![]() 一年来的工作业绩分数的茎叶图如图所示:
一年来的工作业绩分数的茎叶图如图所示:
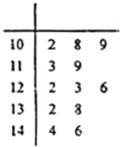
(1)根据职员![]() 的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
的业绩茎叶图求出他这一年的工作业绩的中位数和平均数;
(2)由于职员![]() 的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了六张卡片,其中一张卡片上标注奖金为6千元,两张卡片的奖金为4千元,另外三张的奖金为2千元.规则是:获奖职员
的业绩高,被公司评为年度最佳职员,在公司年会上通过抽奖形式领取奖金.公司准备了六张卡片,其中一张卡片上标注奖金为6千元,两张卡片的奖金为4千元,另外三张的奖金为2千元.规则是:获奖职员![]() 需要从六张卡片中随机抽出两张,这两张卡片上的金额数之和作为奖金数.求职员
需要从六张卡片中随机抽出两张,这两张卡片上的金额数之和作为奖金数.求职员![]() 获得奖金6千元的概率;并说明获得奖金6千元和8千元哪个可能性较大?
获得奖金6千元的概率;并说明获得奖金6千元和8千元哪个可能性较大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com