
【题目】某同学在研究下学习中,关于三角形与三角函数知识的应用(约定三内角![]() ,
,![]() ,
,![]() 的对边分别为
的对边分别为![]() ,
,![]() ,
,![]() )得出如下一些结论:
)得出如下一些结论:
(1)若![]() 是钝角三角形,则
是钝角三角形,则![]() ;
;
(2)若![]() 是锐角三角形,则
是锐角三角形,则![]() ;
;
(3)在三角形![]() 中,若
中,若![]() ,则
,则![]() ;
;
(4)在![]() 中,若
中,若![]() ,
,![]() ,则
,则![]() .其中错误命题的个数是( )
.其中错误命题的个数是( )
A. 0 B. 1 C. 2 D. 3
【答案】D
【解析】分析:由题意结合三角函数的性质逐一分析所给命题的真假即可.
详解:逐一考查所给命题的真假:
(1)∵tanA+tanB=tan(A+B)(1tanAtanB),
∴tanA+tanB+tanC=tan(A+B)(1tanAtanB)+tanC=tanAtanBtanC,
∴△ABC是钝角三角形,可得:tanAtanBtanC<0,故错误;
(2)∵△ABC为锐角三角形,
∴A+B>90°,B>90°A,
∴cosB<sinA,sinB>cosA,
∴cosBsinA<0,sinBcosA>0,
∴cosBsinA<sinBcosA,可得cosA+cosB<sinA+sinB,故错误;
(3)当B=![]() 时,tanB不存在,故错误;
时,tanB不存在,故错误;
(4)由tanC=![]() 得到0<C<90°,且tan30°=
得到0<C<90°,且tan30°=![]() 1=tan45°,
1=tan45°,
因为正切函数在(0,90°)为增函数,所以得到30°<C<45°;
由sinB=![]() 可得到0<B<90°或90°<B<180°,
可得到0<B<90°或90°<B<180°,
在0<B<90°时,sin30°=![]() ,因为正弦函数在(0,90°)为增函数,得到0<B<30°;
,因为正弦函数在(0,90°)为增函数,得到0<B<30°;
在90°<B<180°时,sin150°=![]() ,但是正弦函数在90°<B<180°为减函数,得到B>150°,则B+C>180°,矛盾,不成立。
,但是正弦函数在90°<B<180°为减函数,得到B>150°,则B+C>180°,矛盾,不成立。
所以0<B<30°.由B和C的取值得到A为钝角,
所以A>C>B,故正确;
综上可得,错误命题的个数是3.
本题选择D选项.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:高中数学 来源: 题型:
【题目】 (本小题满分12分)
已知圆C:![]() ,直线
,直线![]() 过定点A (1,0).
过定点A (1,0).
(1)若![]() 与圆C相切,求
与圆C相切,求![]() 的方程;
的方程;
(2)若![]() 与圆C相交于P、Q两点,求三角形CPQ的面积的最大值,并求此时直线
与圆C相交于P、Q两点,求三角形CPQ的面积的最大值,并求此时直线![]() 的方程.
的方程.
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知双曲线 ![]() ,以原点为圆心,双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于
,以原点为圆心,双曲线的实半轴长为半径的圆与双曲线的两条渐近线相交于 ![]() 四点,四边形
四点,四边形 ![]() 的面积为
的面积为 ![]() ,则双曲线的离心率为( )
,则双曲线的离心率为( )
A.![]()
B.2
C.![]()
D.4
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知函数f(x)=ln(x+1)+ax,其中a∈R.
(Ⅰ) 当a=﹣1时,求证:f(x)≤0;
(Ⅱ) 对任意x2≥ex1>0,存在x∈(﹣1,+∞),使 ![]() 成立,求a的取值范围.(其中e是自然对数的底数,e=2.71828…)
成立,求a的取值范围.(其中e是自然对数的底数,e=2.71828…)
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】已知曲线C1:y=cos x,C2:y=sin (2x+![]() ),则下面结论正确的是( )
),则下面结论正确的是( )
A. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
B. 把C1上各点的横坐标伸长到原来的2倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
C. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向右平移
倍,纵坐标不变,再把得到的曲线向右平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
D. 把C1上各点的横坐标缩短到原来的![]() 倍,纵坐标不变,再把得到的曲线向左平移
倍,纵坐标不变,再把得到的曲线向左平移![]() 个单位长度,得到曲线C2
个单位长度,得到曲线C2
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】为评估一种农作物的种植效果,选了n块地作试验田.这n块地的亩产量(单位: ![]() )分别为
)分别为 ![]() ,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
,下面给出的指标中可以用来评估这种农作物亩产量稳定程度的是( )
A.![]() 的平均数
的平均数
B.![]() 的标准差
的标准差
C.![]() 的最大值
的最大值
D.![]() 的中位数
的中位数
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】一次数学考试后,某老师从甲,乙两个班级中各抽取5人,记录他们的考试成绩,得到如图所示的茎叶图,已知甲班5名同学成绩的平均数为81,乙班5名同学成绩的中位数为73,则 ![]() 的值为( )
的值为( )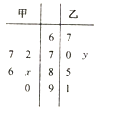
A.2
B.-2
C.3
D.-3
查看答案和解析>>
科目:高中数学 来源: 题型:
【题目】某同学用“五点法”画函数![]() 在某一个周期内的图像时,列表并填入了部分数据,如下表:
在某一个周期内的图像时,列表并填入了部分数据,如下表:
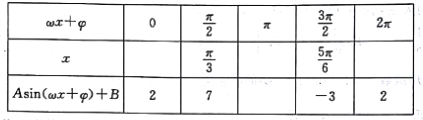
(I)请将上表数据补充完整,并直接写出函数![]() 的解析式
的解析式
(II)将![]() 的图像上所有点向左平行移动
的图像上所有点向左平行移动![]() 个单位长度,得到
个单位长度,得到![]() 的图像,求
的图像,求![]() 的图像离
的图像离![]() 轴最近的对称中心.
轴最近的对称中心.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com